如图，在四边形ABCD中，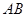
∥
，
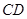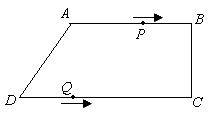
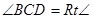，AB=AD=10cm，BC=8cm．点P从点A出发，以每秒3cm的速度沿折线ABCD方向运动，点Q从点D出发，以每秒2cm的速度沿线段DC方向向点C运动．已知动点P、Q同时发，当点Q运动到点C时，P、Q运动停止，设运动时间为
。
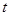求CD的长；
当四边形PBQD为平行四边形时，求四边形PBQD的周长；
在点P、点Q的运动过程中，是否存在某一时刻，使得
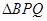的面积为20
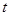，若存在，请求出所有满足条件的的值；若不存在，请说明理由。
已知
，求
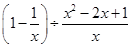的值．
化简：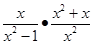
某巡警骑摩托车在一条南北大道上巡逻，某天他从A处出发，晚上停留在B处，规定向北方向为正，当天行驶情况记录如下（单位：千米）：
+10，－8，+7，－15，+6，－16，+4，－2
（1）B处在A处何方？距离A处多远？
（2）若摩托车每行驶1千米耗油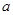
升，这一天共耗油多少升？
有10箱苹果，标准质量是每箱25千克，每箱质量与标准质量的差值（单位：千克）
如下：0.25，0，-0.4，0，0，0.2，0.3，-0.3，0，0.苹果总共有多少千克？
某地探空气球的气象观测资料表明，高度每增加1千米，气温下降大约6℃，若该地区地面温度为23℃，该地区高空某点温度为-31℃，则此点的高度是大约是多少千米？