设函数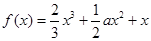 ,
,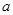 ∈R
∈R
(1)当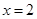 时,
时,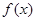 取得极值,求
取得极值,求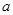 的值;
的值;
(2)若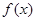 在
在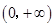 内为增函数,求
内为增函数,求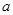 的取值范围.
的取值范围.
在某大学自主招生考试中,所有选报II类志向的考生全部参加了数学与语文两个科目的考试,成绩分为A,B,C,D,E五个等级,某考场考生的两科考试成绩的数据统计如下图,已知该考场中数学科目成绩为B的考生有10人.
(1)求该考场考生中语文科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分,求该考场考生数学科目平均分;
(3)已知本考场考生中,恰有2人的两科成绩均为A,在至少一科成绩为A的考生中,随机抽取2人进行访谈,求这2人的两科成绩均为A的概率.
已知 中,a,b,c 为角A,B,C 所对的边,
中,a,b,c 为角A,B,C 所对的边, .
.
(1)求cos A的值;
(2)若 的面积为
的面积为 ,求b ,c 的长.
,求b ,c 的长.
已知数列 是公差大于零的等差数列,数列
是公差大于零的等差数列,数列 为等比数列,且
为等比数列,且

(1)求数列 和
和 的通项公式
的通项公式
(2)设 ,求数列
,求数列 前n项和
前n项和 .
.
已知函数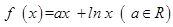 .
.
(1)若a=2,求曲线y=f(x)在x=1处的切线方程;
(2)求f(x)的单调区间;
(3)设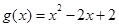 ,若对任意
,若对任意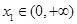 ,均存在
,均存在 ,使得
,使得 ,求a的取值范围.
,求a的取值范围.
已知椭圆E: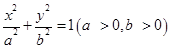 的离心率
的离心率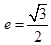 ,并且经过定点
,并且经过定点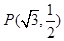
(1)求椭圆E 的方程;
(2)问是否存在直线y=-x+m,使直线与椭圆交于A, B 两点,满足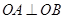 ,若存在求m 值,若不存在说明理由.
,若存在求m 值,若不存在说明理由.