袋子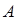
和
中装有若干个均匀的红球和白球，从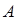中摸一个红球的概率是
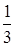，从中摸出一个红球的概率为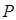
.
⑴从A中有放回地摸球，每次摸出一个，有3次摸到红球则停止.
① 求恰好摸5次停止的概率；
② 记5次之内（含5次）摸到红球的次数为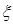
，求随机变量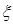的分布列及数学期望
.
⑵若A、B两个袋子中的球数之比为1：2，将A、B中的球装在一起后，从中摸出一个红球的概率是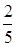
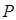，求的值.
（本大题满分12分）已知函数f(x)=
(x≠-a,a≠
).
(1)求f(x)的反函数； (2)若函数
的图象关于y=x对称，求a的值.。
（本小题满分13分）
已知函数
，其中
为自然对数的底数．
（I）求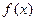
的最小值；
（II）设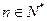
，且
，证明：
．
（本小题满分14分）
从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业．根据规划，第1年投入800万元，以后每年的投入将比上一年减少
；当年旅游业收八为400万元，预计今后的旅游业收入每年会比上一年增加
．
（I）设
年的总投入为
万元，旅游业总收入为
万元，写出，的表达式；
（II）至少经过多少年，旅游业的总收入才能超过总投入？（计算时取
）
（本小题满分14分）
已知函数
．
（I）当
时，求曲线
在点
处切线的斜率；
（II）当
时，求函数
的单调区间．
（本小题满分13分）
已知函数
，其中
．
（I）在给定的坐标系中，画出函数
的图象；
（II）设
，且
，证明：
．