（本小题满分14分）
从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业．根据规划，第1年投入800万元，以后每年的投入将比上一年减少
；当年旅游业收八为400万元，预计今后的旅游业收入每年会比上一年增加
．
（I）设
年的总投入为
万元，旅游业总收入为
万元，写出，的表达式；
（II）至少经过多少年，旅游业的总收入才能超过总投入？（计算时取
）
已知向量：a＝(2sinx,2 sinx)，b＝(sinx，
cosx)．
为常数）
（1）若
，求
的最小正周期；
（2）若在[
上最大值与最小值之和为5，求t的值；
（3）在（2）条件下先按
平移后（︱︱最小）再经过伸缩变换后得到
求.
已知方程x2＋y2－2(m＋3)x＋2(1－4m2)y＋16m4＋9＝0表示一个圆．
(1)求实数m的取值范围；(2)求该圆半径r的取值范围；(3)求圆心的轨迹方程．
已知集合A=
B=
（1）当m=3时，求A
(
RB)；
（2）若AB 
，求实数m的值.
（本小题满分15分）已知直线l的方程为：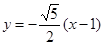
，直线l与x轴的交点为F， 圆O的方程为：
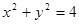，C、 D在圆上， CF⊥DF，设线段CD的中点为M．
（1）如果CFDG为平行四边形，求动点G的轨迹；
（2）已知椭圆的中心在原点，右焦点为F，直线l交椭圆于A、B两点，又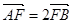
，
求椭圆C的方程．
（本小题满分15分）
函数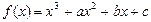
，曲线
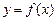上点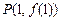
处的切线方程为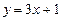
（1）若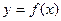
在
时有极值，求函数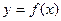在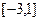
上的最大值；
（2）若函数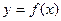在区间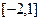
上单调递增，求
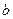的取值范围．