某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
| |
积极参加班级工作 |
不太主动参加班级工作 |
合计 |
| 学习积极性高 |
18 |
7 |
25 |
| 学习积极性一般 |
6 |
19 |
25 |
| 合计 |
24 |
26 |
50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?说明理由.
 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
给定抛物线C:y2=4x,F是C的焦点,过点F的直线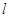 与C相交于A、B两点。
与C相交于A、B两点。
(1)设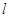 的斜率为1,求
的斜率为1,求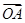 与
与 夹角的余弦值;
夹角的余弦值;
(2)设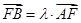 ,若
,若 ∈[4,9],求
∈[4,9],求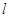 在y轴上截距的变化范围。
在y轴上截距的变化范围。
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB= PD.
PD.
(I)证明: 平面
平面 (II)证明:平面PQC⊥平面DCQ
(II)证明:平面PQC⊥平面DCQ 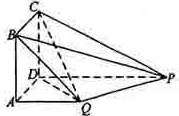
如图,圆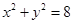 内有一点P(-1,2),弦AB为过点P.
内有一点P(-1,2),弦AB为过点P.
(1) 当弦AB被点P平分时,求出直线AB的方程;
(2) 设过P点的弦的中点为 ,求点
,求点 的坐标所满足的关系式.
的坐标所满足的关系式.
.已知 ,设
,设 在R上单调递减,
在R上单调递减, 的值域为R,如果“
的值域为R,如果“ 或
或 ”为真命题,“
”为真命题,“ 或
或 ”也为真命题,求实数
”也为真命题,求实数 的取值范围。
的取值范围。
.设椭圆E: 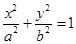 (a,b>0)过M(2,
(a,b>0)过M(2, ) ,N(
) ,N(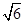 ,1)两点,O为坐标原点,(I)求椭圆E的方程;
,1)两点,O为坐标原点,(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。