为缓解油价上涨给出租车行业带来的成本压力,某巿自2012年5月1日起,调
为缓解油价上涨给出租车行业带来的成本压力,某巿自2012年5月1日起,调整出租车运价,调整方案见下列表格及图像(其中a,b为常数).
| 行驶路程 |
收费标准 |
|
| 调价前 |
调价后 |
|
| 不超过3km的部分 |
起步价6元 |
起步价a元 |
| 超过3km的部分 |
每公里2.1元 |
每公里b元 |
设行驶路程x km时,调价前的运价为y1(元),调价后的运价为y2(元).如图,折线ABC表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题: 填空:a= , b= .
写出当x>3时,y1与x的函数关系式,并在上图中画出该函数的图象.
函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.

(·湖北荆门,21题,分)如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).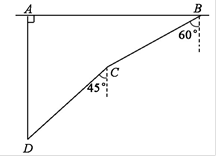
(·湖北鄂州,21题,9分)如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量 ,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).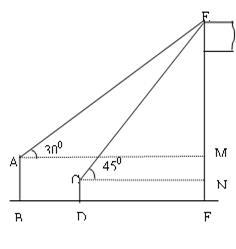
(1)求小敏到旗杆的距离DF.(结果保留根号)
(2)求旗杆EF的高度.(结果保留整数. 参考数据:
参考数据: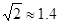 ,
,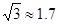 )
)
(·湖南益阳)如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.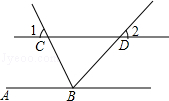
(·湖南株洲)某学校举行一次体育测试,从所有参加测试的学生中随机抽取10名学生的成绩,制作出如下统计表和条形统计图:
| 编号 |
成绩 |
等级 |
编号 |
成绩 |
等级 |
| 95 |
A |
⑥ |
76 |
B |
|
| 78 |
B |
⑦ |
85 |
A |
|
| 72 |
C |
⑧ |
82 |
B |
|
| 79 |
B |
⑨ |
77 |
B |
|
| 92 |
A |
⑩ |
69 |
C |
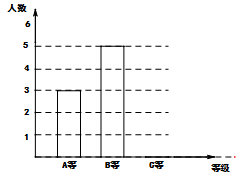
请回答下列问题:
(1)孔明同学这次测试的成绩是87分,则他的成绩等级是 ;
(2)请将条形统计图补充完整;
(3)已知该校所有参加这次测试的学生中,有60名学生成绩是A等,请根据以上抽样结果,估计该校参加这次测试的学生总人数是多少?
(·湖南益阳)2014年益阳市的地区生产总值(第一、二、三产业的增加值之和)已进入千亿元俱乐部,如图表示2014年益阳市第一、二、三产业增加值的部分情况,请根据图中提供的信息解答下列问题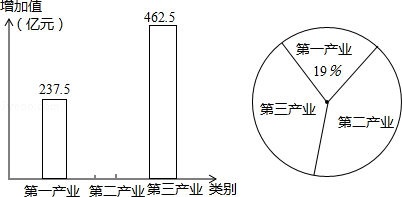
(1)2014年益阳市的地区生产总值为多少亿元?
(2)请将条形统计图中第二产业部分补充完整;
(3)求扇形统计图中第二产业对应的扇形的圆心角度数.