已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,3)三点,连接AB,过点B作BC∥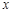 轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动,动点E、F有一个点到达目的点即停止全部运动.设动点运动的时间为t(秒).
轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动,动点E、F有一个点到达目的点即停止全部运动.设动点运动的时间为t(秒).
求抛物线的解析式
记△EFA的面积为S,求S关于t的函数关系式,并求S的最大值;
是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时点E的坐标;若不存在,请说明理由.
先化简,再求值:
(1) ,其中:
,其中: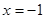 ,
, 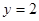 .
.
(2)已知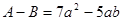 ,且
,且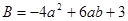 .
.
①求A等于多少;②若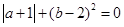 ,求A的值.
,求A的值.
(3)已知多项式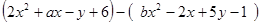 .
.
①若多项式的值与字母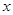 的取值无关,求
的取值无关,求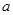 、
、 的值;
的值;
②在①的条件下,先化简多项式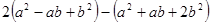 ,再求它的值.
,再求它的值.
化简:(1)
(2)
(共18分)计算:
(1)
(2)
(3)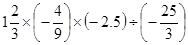
(4)
(5)
(6)
从2开始,连续的偶数相加,它们和的情况如下表:
(1)如果n=8时,那么S的值为________;
(2)由表中的规律猜想:用n的代数式表示S的公式为S=2+4+6+8+…+2n=_________;
(3)由上题的规律计算300+302+304+…+2010+2012的值(要有计算过程).
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:A→B(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中:
(1)A→C( , ),B→D( , );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+1,-1),(-2,+3),(-1,-2),请在图中标出P的位置.