如图,某人在山坡坡脚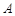 处测得电视塔尖点
处测得电视塔尖点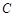 的仰角为
的仰角为 ,沿山坡向上走到
,沿山坡向上走到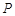 处再测得点
处再测得点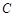 的仰角为
的仰角为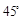 ,已知
,已知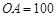 米,山坡坡度
米,山坡坡度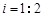 且O 、A、B在同一条直线上.求电视塔
且O 、A、B在同一条直线上.求电视塔 的高度以及此人所在位置点
的高度以及此人所在位置点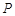 的铅直高度.(测倾器高度忽略不计,结果保留根号形式)
的铅直高度.(测倾器高度忽略不计,结果保留根号形式)
在数轴上把下列各数表示出来,并按照由小到大的顺序进行排列.
0、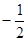 、3、-2.5 、
、3、-2.5 、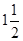
如图,抛物线y=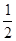 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).⑴求抛物线的解析式及顶点D的坐标;
判断△ABC的形状,证明你的结论;
点M(m,0)是x
 轴上的一个动点, 当CM+DM的值最小时,求m的值.
轴上的一个动点, 当CM+DM的值最小时,求m的值.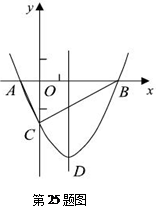
在数学活动课上,同学们用一根长为1米的细绳围矩形.)小明围出了一个面积为600㎝2的矩形,请你算一算,她围成的矩形的长和宽各是多少?
小颖想用这根细绳围成一个面积尽可能大的矩形,请你用所学过的知识帮他分析应该怎么围,并求出最大面积
先化简,再求值: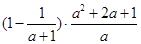 ,其中a =
,其中a =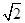 -1.
-1.
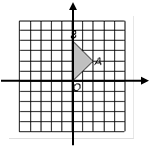
如图,正方形网格中的每个小正方形的边长都是1,在 平面直角坐标系中,已知,ΔABO的三个顶点的坐标分别为A(2,2),B(0,4),O(0,0);
平面直角坐标系中,已知,ΔABO的三个顶点的坐标分别为A(2,2),B(0,4),O(0,0); 画出ΔABO绕点O逆时针旋转900后得到的Δ
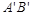 0并写出点A
0并写出点A ,B
,B 的坐标;
的坐标;求旋转过程中动点B所经过的路径长。