如图，在平面直角坐标系中，直线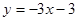
与
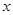轴交于点A，与y轴交于点C. 抛物线
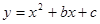经过A、C两点，且与x轴交于另一点B(点B在点A右侧).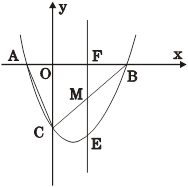
求抛物线的解析式及点B坐标；
若点M是线段BC上一动点，过点M的直线EF平行y轴交
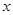轴于点F，交抛物线于点E.求ME长的最大值；试探究当ME取最大值时，在抛物线x轴下方是否存在点P，使以M、F、B、P为顶点的四边形是平行四边形？若存在，请求出点P的坐标；若不存在，试说明理由.
如图，在三角形ABC中，以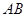
为直径作⊙O，交AC于点E，OD⊥AC于D，∠AOD=∠C．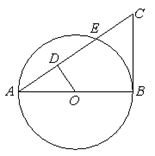
（1）求证：BC为⊙O的切线；
（2）若
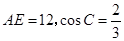，求OD的长．
如图，抛物线与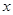
轴交于A(1，0)，B（
，0）两点，与
轴交于点C(0，3)．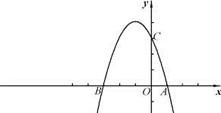
(1)求此抛物线的解析式；
(2)在x轴上找一点D，使得以点A、C、D为顶点的三角形是直角三角形，求点D的坐标．
某超市按每袋20元的价格购进某种干果．销售过程中发现，每月销售量y（袋）与销售单价x（元）之间的关系可近似地看作一次函数：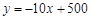
（
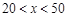）．（1）当x=45元时，y=袋；当y=200袋时，x=元；
（2）设这种干果每月获得的利润为w（元），当销售单价定为多少元时，每月可获得最大利润？最大利润是多少?
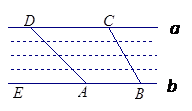
如图，河两岸a，b互相平行，C，D是河岸a上间隔40米的两根电线杆，某人在河岸b上的A处，测得∠DAE=45°，然后沿河岸走了30米到达B处，测得∠CBE=60°，求河的宽度（结果精确到1米，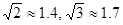
）．
袋中装有编号为1，2，3的三个质地均匀、大小相同的球，从中随机取出一球记下编号后，放入袋中搅匀，再从袋中随机取出一球，记下编号．将两次编号作为数字求和．（1）请用树状图或列表的方法表示可能出现的所有结果；
（2）求两次所取球的编号之和是偶数的概率．