如图,A、B两个转盘均被平均分成三个扇形,分别转动A盘、B盘各一次.转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.小敏分别转动两个转盘, 当两个转盘停止后,小敏把A转盘指针所指区域内的数字记为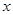 ,B转盘指针所指区域内的数字记为
,B转盘指针所指区域内的数字记为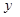 .这样就确定了点P的坐标
.这样就确定了点P的坐标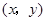 .(1)用列表或画树状图的方法写出点P的所有可能坐标;(2)求点P落在坐标轴上的概率.
.(1)用列表或画树状图的方法写出点P的所有可能坐标;(2)求点P落在坐标轴上的概率.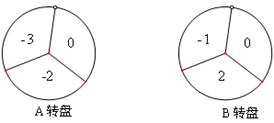
郑州市花卉种植专业户王有才承包了30亩花圃,分别种植康乃馨和玫瑰花,有关成本、销售额见下表:
| 种植种类 |
成本(万元/亩) |
销售额(万元/亩) |
| 康乃馨 |
2.4 |
3 |
| 玫瑰花 |
2 |
2.5 |
(1)2012年,王有才种植康乃馨20亩、玫瑰花10亩,求王有才这一年共收益多少万元?(收益=销售额-成本)
(2)2013年,王有才继续用这30亩花圃全部种植康乃馨和玫瑰花,计划投入成本不超过70万元.若每亩种植的成本、销售额与2012年相同,要获得最大收益,他应种植康乃馨和玫瑰花各多少亩?
(3)已知康乃馨每亩需要化肥500kg,玫瑰花每亩需要化肥700kg,根据(2)中的种植亩数,为了节约运输成本,实际使用的运输车辆每次装载化肥的总量是原计划每次装载总量的2倍,结果运输全部化肥比原计划减少2次.求王有才原定的运输车辆每次可装载化肥多少千克?
某学校为了绿化校园,决定从某苗圃购进甲、乙、丙三种树苗共80株,其中甲种树苗株树是乙种树苗株树的2倍,购买三种树苗的总金额不超过1320元,已知乙种树苗的单价是16元/株,乙种树苗的单价是甲种树苗的单价的 ,购买丙种树苗12株的金额等于购买甲种树苗20株的金额。
,购买丙种树苗12株的金额等于购买甲种树苗20株的金额。
(1)甲、丙两种树苗的单价分别是多少元?
(2)若要求甲种树苗的株树不超过丙种树苗的株树,请你帮助设计共有哪些购买方案?
阅读理解: 对非负实数x“四舍五入”到个位的值记为<x>,
即:当n为非负整数时,如果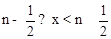 ,则<x>=n。
,则<x>=n。
如:<0>=<0.49>=0,<0.64>=<1.393>=1,<3>=3,<2.5>=<3.12>=3,…
试解决下列问题:
(1)填空:如果<3x-2>=4,则实数x的取值范围为 ;
(2)当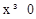 ,m为非负整数时,求证:
,m为非负整数时,求证: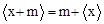 ;
;
(3)求满足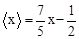 的所有非负实数x的值;
的所有非负实数x的值;
某校为了丰富学生的校园生活,准备购进一批价格分别为80元、60元的篮球和足球。该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
已知 x1、x2是一元二次方程 的两个实数根。
的两个实数根。
(1)求 的取值范围;
的取值范围;
(2)是否存在实数 ,使
,使 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。