现有8名奥运会志愿者,其中志愿者 通晓日语,
通晓日语, 通晓俄语,
通晓俄语,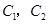 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(Ⅰ)求 被选中的概率;
被选中的概率;
(Ⅱ)求 和
和 不全被选中的概率.
不全被选中的概率.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,-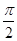 <φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
<φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).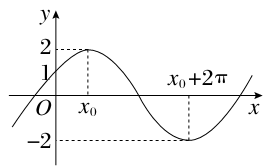
(1)求函数f(x)的解析式;
(2)若锐角θ满足cosθ=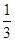 ,求f(2θ)的值.
,求f(2θ)的值.
已知函数f(x)=2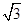 cos2x+sin2x-
cos2x+sin2x-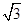 +1(x∈R).
+1(x∈R).
(1)求f(x)的最小正周期;
(2)求f(x)的单调递增区间;
(3)若x∈[-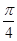 ,
,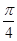 ],求f(x)的值域.
],求f(x)的值域.
已知函数f(x)=2cosxsin(x+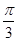 )-
)-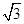 sin2x+sinxcosx.
sin2x+sinxcosx.
(1)求函数f(x)的单调递减区间;
(2)将函数f(x)的图象沿x轴向右平移m个单位后的图象关于直线x=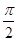 对称,求m的最小正值.
对称,求m的最小正值.
已知a>0,函数f(x)=-2asin(2x+ )+2a+b,当x∈[0,
)+2a+b,当x∈[0,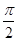 ]时,-5≤f(x)≤1.
]时,-5≤f(x)≤1.
(1)求常数a,b的值;
(2)设g(x)=f(x+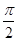 )且lg[g(x)]>0,求g(x)的单调区间.
)且lg[g(x)]>0,求g(x)的单调区间.
设函数f(x)=sin(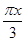 -
-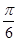 )-2cos2
)-2cos2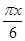 .
.
(1)求y=f(x)的最小正周期及单调递增区间;
(2)若函数y=g(x)与y=f(x)的图象关于直线x=2对称,求当x∈[0,1]时,函数y=g(x)的最大值.