在平面直角坐标系xOy中，抛物线
经过点N（2,－5），过点N作x轴的平行线交此抛物线左侧于点M，MN=6.求此抛物线的解析式
点P（x,y）为此抛物线上一动点，连接MP交此抛物线的对称轴于点D，当△DMN为直角三角形时，求点P的坐标；
设此抛物线与y轴交于点C，在此抛物线上是否存在点Q，使∠QMN=∠CNM ？若存在，求出点Q的坐标；若不存在，说明理由.
为了加强食品安全管理，有关部门对某大型超市的甲、乙两种品牌食用油共抽取18瓶进行检测，检测结果分成“优秀”、“合格”、“不合格”三个等级，数据处理后制成以下折线统计图和扇形统计图．
⑴甲、乙两种品牌食用油各被抽取了多少瓶用于检测？
⑵在该超市购买一瓶乙品牌食用油，请估计能买到“优秀”等级的概率是多少？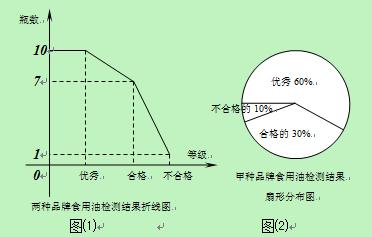
解方程：
如图，已知O是平面直角坐标系的原点，半径为1的⊙B经过点O，且与x、y
轴分别交于点A、C，点A的坐标为（-，0），AC的延长线与⊙B的切线OD
交于点D.
（1）求OC的长和∠CAO的度数；
（2）求点D的坐标；
（3）求过点A，O，D三点的抛物线的解析式；
（4）在（3）中，点P是抛物线上的一点，试确定点P的位置，使得△AOP的
面积与△AOC的面
积相等.
在△ABC中，BC=6，AC=4，∠C=45o，在BC上有一动点P，过P作PD∥BA与AC相交于点D，连结AP，设BP=x，△APD的面积为y.
（1）求y与x之间的函数关系式，并指出自变量x的取值范围；
（2）是否存在点P，使△APD的面积最大？若存在，求出BP的长，并求出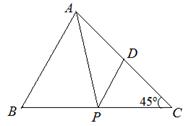
△APD面积的最大值.
一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部，每款手机至少要购进8部，且恰好用完购机款61000元．设购进A型手机x部，B型手机y部．三款手机的进价和预售价如下表：
| 手机型号 |
A型 |
B型 |
C型 |
| 进价（单位：元/部） |
900 |
1200 |
1100 |
| 预售价（单位：元/部） |
1200 |
1600 |
1300 |
（1）用含x，y的式子表示购进C型手机的部数；
（2）求出y与x之间的函数关系式；
（3）假设所购进手机全部售出，综合考虑各种因素，该手机经销商在购销这批手机过程中需另外支出各种费用共1500元．
①求出预估利润P（元）与x（部）的函数关系式；（注：预估利润P＝预售总额-购机款-各种费用）
②求出预估利润的最大值，并写出此时购进三款手机各多少部．