如图,已知三棱锥 中,
中,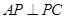 ,
, ,
,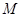 为
为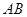 中点,
中点, 为
为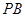 中点,且
中点,且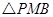 是正三角形.
是正三角形.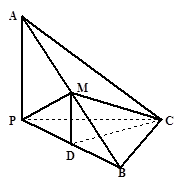
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)若 ,
,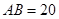 ,求三棱锥
,求三棱锥 的体积.
的体积.
(本小题7分)已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=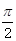 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).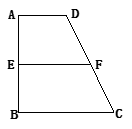
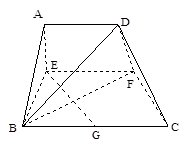
(1)当x=2时,求证:BD⊥EG ;
(2)若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
已知命题:“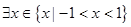 ,使等式
,使等式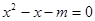 成立”是真命题.
成立”是真命题.
(1)求实数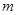 的取值集合
的取值集合 ;
;
(2)设不等式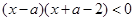 的解集为
的解集为 ,若
,若 是
是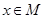 的必要条件,求
的必要条件,求 的取值范围.
的取值范围.
数列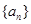 的前n项和为
的前n项和为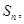 且
且 设
设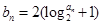 ,
, 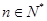 .
.
(1)求数列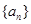 的通项公式;
的通项公式;
(2)求数列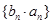 的前n项和
的前n项和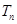 ;
;
(3)证明:对于任意 ,不等式
,不等式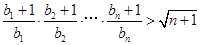 恒成立.
恒成立.
设椭圆C: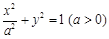 的两个焦点是
的两个焦点是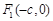 和
和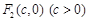 ,且椭圆C与圆
,且椭圆C与圆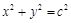 有公共点,
有公共点,
(1)求a的取值范围;
(2)若椭圆上的点到焦点的最短距离为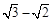 ,求椭圆方程.
,求椭圆方程.
已知圆O: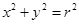 上的点到直线
上的点到直线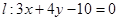 的最小距离为1,设P为直线
的最小距离为1,设P为直线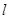 上的点,过P点作圆O的两条切线PA、PB, 其中A、B为切点.
上的点,过P点作圆O的两条切线PA、PB, 其中A、B为切点.
(1)求圆O的方程;
(2)当点P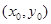 为直线
为直线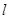 上的定点时,求直线AB的方程.
上的定点时,求直线AB的方程.