已知函数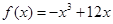 ,①求函数的单调区间;②求函数的极值,③当
,①求函数的单调区间;②求函数的极值,③当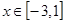 时,求函数的最大值与最小值.
时,求函数的最大值与最小值.
设全集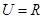 ,
,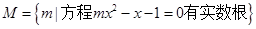 ,
,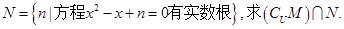
已知集合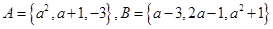 ,若
,若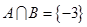 ,求实数
,求实数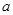 的值。
的值。
如图1,在直角梯形ABCD中,AD∥BC,顶点D,C分别在AM,BN上运动(点D不与A重合,点C不与B重合),E是AB上的动点(点E不与A,B重合),在运动过程中始终保持DE⊥CE,且AD+DE=AB=a.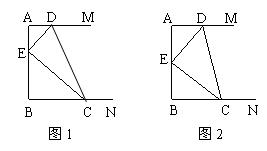
(1)求证:△ADE∽△BEC;
(2)设AE=m,请探究:△BEC的周长是否与m值有关,若有关请用含m的代数式表示△BEC的周长;若无关请说明理由.
为了鼓励居民节约用水,我市某地水费按下表规定收取:
| 每户每月用水量 |
不超过10吨(含10吨) |
超过10吨的部分 |
| 水费单价 |
1.30元/吨 |
2.00元/吨 |
(1)某用户用水量为x吨,需付水费为y元,则水费y(元)与用水量x(吨)之间的函数关系式是 ;
;
(2)若小华家四月份付水费17元,问他家四月份用水多少吨?
(3)已知某住宅小区100户居民五月份交水费1682元,且该月每户用水量均不超过15吨(含15吨),求该月用水量不超过10吨的居民最多可能有多少户?
如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF.
(1)求证:AF=CE;
(2)若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论.