某单位要在甲、乙、丙、丁4人中安排2人分别担任周六、周日的值班任务(每人被安排是等可能的,每天只安排一人).
(1)共有多少种安排方法?
(2)其中甲、乙两人都被安排的概率是多少?
(3)甲、乙两人中至少有一人被安排的概率是多少?
(本题满分12分)双曲线与椭圆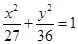 有相同焦点,且经过点(
有相同焦点,且经过点(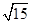 ,4),求其方程.
,4),求其方程.
(本小题满分14分)已知动圆 过定点
过定点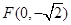 ,且与直线
,且与直线 相切,椭圆
相切,椭圆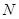 的对称轴为坐标轴,一个焦点为
的对称轴为坐标轴,一个焦点为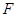 ,点
,点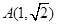 在椭圆
在椭圆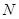 上.
上.
(1)求动圆圆心 的轨迹
的轨迹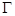 的方程及椭圆
的方程及椭圆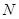 的方程;
的方程;
(2)若动直线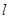 与轨迹
与轨迹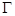 在
在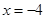 处的切线平行,且直线
处的切线平行,且直线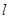 与椭圆
与椭圆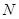 交于
交于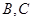 两点,试求当
两点,试求当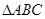 面积取到最大值时直线
面积取到最大值时直线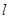 的方程.
的方程.
(本小题满分12分)已知函数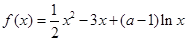 ,
, ,
,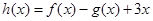 ,其中
,其中 且
且 .
.
(I)求函数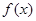 的导函数
的导函数 的最小值;
的最小值;
(II)当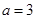 时,求函数
时,求函数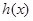 的单调区间及极值;
的单调区间及极值;
(III)若对任意的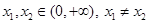 ,函数
,函数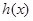 满足
满足 ,求实数
,求实数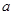 的取值范围.
的取值范围.
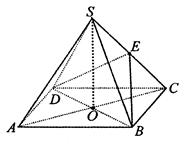
如图,四棱锥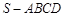 中,底面
中,底面 是边长为4的正方形,
是边长为4的正方形, 是
是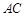 与
与 的交点,
的交点,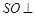 平面
平面 ,
,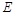 是侧棱
是侧棱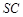 的中点,异面直线
的中点,异面直线 和
和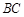 所成角的大小是60
所成角的大小是60 .
.
(Ⅰ)求证:直线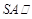 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)已知函数 (
( ),直线
),直线 ,
, 是
是 图象的任意两条对称轴,且
图象的任意两条对称轴,且 的最小值为
的最小值为 .
.
(I)求 的表达式;
的表达式;
(Ⅱ)将函数 的图象向右平移
的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数 的图象,若关于
的图象,若关于 的方程
的方程 ,在区间
,在区间 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数 的取值范围.
的取值范围.