在△
中，AD⊥BC，
（1）利用尺规作图，作△
外接圆⊙O；
（2）判断：AC和⊙O的位置关系,并说明理由；
（3）若AC=10，AD=8，求⊙O的直径；
小玲用下面的方法来测量学校教学大楼AB的高度：如图，在水平地面上放一面平面镜，镜子与教学大楼的距离EA=21米．当她与镜子的距离CE=2．5米时，她刚好能从镜子中看到教学大楼的顶端B．已知她的眼睛距地面高度DC=1．6米．请你帮助小玲计算出教学大楼的高度AB是多少米（注意：根据光的反射定律：反射角等于入射角）．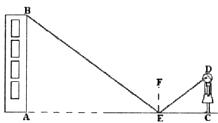
（本题满分l0分）
如图，AB是⊙O的直径，BC是弦，OD⊥BC于E，交弧BC于D．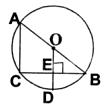
（1）请写出四个不同类型的正确结论；
①_____________；②__________；③__________；④______．（2）若BC=8，ED=2，求⊙O的半径．
如图，已知△ADE和△ABC是位似图形，∠A=30°，DE垂直平分AC，且DE=2．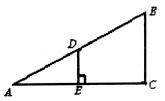
（1）求∠C的度数．
（2）求BC的长度．
请判断关于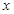
的一元二次方程
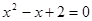的根的情况，并说明理由．如果方程有根，请写出方程的根；如果没有根，请通过只改变常数项的值，写出一个有实数根的一元二次方程．
在一个口袋中有3个完全相同的小球，把它们分别标号为1、2、3，随机地摸取一个小球后放回，再随机地摸出一个小球，求“两次取的小球的标号相同”的概率，请借助列表法或树形图说明理由．