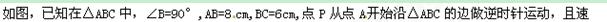在函数中,我们把关于x的一次函数
与
称为一对交换函数，如
与
是一对交换函数.称函数是函数的交换函数.
（1）求函数y＝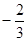
x＋4与交换函数的图像的交点坐标；
（2）若函数y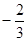＝x＋b（b为常数）与交换函数的图像及纵轴所围三角形的面积为4,求b 的值．
如图，已知：在等边三角形ABC中，D、E分别在AB和AC上，且AD="CE" ，BE和CD相交于点P。说明△ACD≌△CEB
求：∠BPD 的度数.
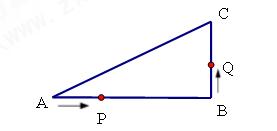
如图，滑杆在机械槽内运动，∠ACB为直角，已知滑杆AB 长2.5米，顶端A在AC 上运动，量得滑杆下端B距C点的距离为1.5米，当端点B向右移动0.5米时，求滑杆顶端A下滑多少米？
如图，在△ABC中，∠B=∠C， AD是△ABC的BC边上的高，DE∥AB，交AC于点E，判断△ADE是不是等腰三角形，并说明理由。
我们在七年级（下）中学习了三角形的内角和等于180°，当时，我们是通过拼图的方
法得到的。现在你能否利用平行线的性质来得出“三角形的内角和等于180°”？请你添上辅助线并把过程写下来。
