已知数列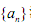 满足:
满足: ,且
,且
(1)求通项公式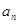
(2)设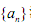 的前n项和为S n,问:是否存在正整数m、n,使得
的前n项和为S n,问:是否存在正整数m、n,使得
若存在,请求出所有的符合条件的正整数对(m,n),若不存在,请说明理由.
(本小题满分12分)从广州某高校男生中随机抽取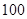 名学生,测得他们的身高(单位: cm)情况如表1:
名学生,测得他们的身高(单位: cm)情况如表1:
| 分组 |
频数 |
频率 |
 |
 |
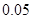 |
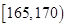 |
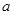 |
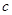 |
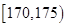 |
 |
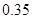 |
 |
 |
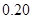 |
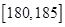 |
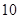 |
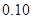 |
| 合计 |
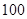 |
 |
表1
(1)求 的值;
的值;
(2)按表1的身高组别进行分层抽样, 从这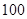 名学生中抽取
名学生中抽取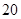 名担任广州国际马拉松志愿者, 再从身高不低于
名担任广州国际马拉松志愿者, 再从身高不低于 cm的志愿者中随机选出
cm的志愿者中随机选出 名担任迎宾工作, 求这
名担任迎宾工作, 求这 名担任迎宾工作的志愿者中至少有
名担任迎宾工作的志愿者中至少有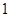 名的身高不低于
名的身高不低于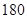 cm的概率.
cm的概率.
(本小题满分12分)已知函数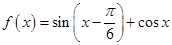 .
.
(1)求函数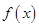 的最小正周期;
的最小正周期;
(2)若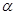 是第一象限角,且
是第一象限角,且 ,求
,求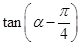 的值.
的值.
(本小题满分14分)已知函数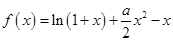
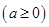 .
.
(1)若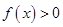 对
对 都成立,求
都成立,求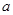 的取值范围;
的取值范围;
(2)已知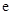 为自然对数的底数,证明:
为自然对数的底数,证明: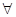
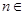 N
N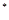 ,
,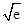
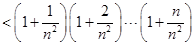
 .
.
(本小题满分14分)已知椭圆 的中心在坐标原点,两焦点分别为双曲线
的中心在坐标原点,两焦点分别为双曲线 的顶点,直线
的顶点,直线 与椭圆
与椭圆 交于
交于 ,
, 两点,且点
两点,且点 的坐标为
的坐标为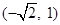 ,点
,点 是椭圆
是椭圆 上异于点
上异于点 ,
, 的任意一点,点
的任意一点,点 满足
满足 ,
, ,且
,且 ,
, ,
, 三点不共线.
三点不共线.
(1)求椭圆 的方程;
的方程;
(2)求点 的轨迹方程;
的轨迹方程;
(3)求 面积的最大值及此时点
面积的最大值及此时点 的坐标.
的坐标.
(本小题满分14分)已知数列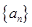 的各项均为正数,其前
的各项均为正数,其前 项和为
项和为 ,且满足
,且满足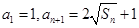 ,
,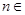 N
N .
.
(1)求 的值;
的值;
(2)求数列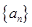 的通项公式;
的通项公式;
(3)是否存在正整数 , 使
, 使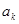 ,
, 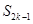 ,
, 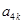 成等比数列? 若存在, 求
成等比数列? 若存在, 求 的值; 若不存在, 请说明理由.
的值; 若不存在, 请说明理由.