如图所示,公园内有一块边长为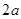 的等边
的等边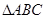 形状的三角地,现修成草坪,图中
形状的三角地,现修成草坪,图中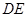 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分,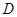 在
在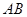 上,
上, 在
在 上.
上.
(Ⅰ)设
 ,试用
,试用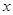 表示
表示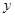 的函数关系式;
的函数关系式;
(Ⅱ)如果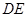 是灌溉水管,为节约成本希望它最短,
是灌溉水管,为节约成本希望它最短,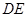 的位置应该在哪里?如果
的位置应该在哪里?如果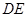 是参观线路,则希望它最长,
是参观线路,则希望它最长,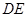 的位置又在哪里?请给予证明.
的位置又在哪里?请给予证明.
(本小题满分12分)设函数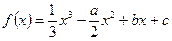 ,其中
,其中 ,曲线
,曲线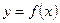 在点
在点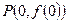 处的切线方程为
处的切线方程为 轴
轴
(1)若 为
为 的极值点,求
的极值点,求 的解析式
的解析式
(2)若过点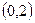 可作曲线
可作曲线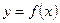 的三条不同切线,求
的三条不同切线,求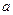 的取值范围。
的取值范围。
(本小题满分12分)已知函数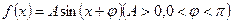 ,
, 的最小值是
的最小值是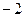 ,其图像经过点
,其图像经过点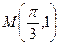 .(1)求
.(1)求 的解析式;(2)已知
的解析式;(2)已知 ,且
,且 ,
,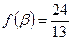 ,求
,求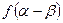 的值.
的值.
(本小题满分12分)通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用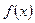 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力(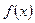 的值越大,表示接受能力越强),
的值越大,表示接受能力越强), 表示提出和讲授概念的时间(单位:分),可以有以下公式:
表示提出和讲授概念的时间(单位:分),可以有以下公式: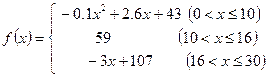
(1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)开讲 分钟与开讲
分钟与开讲 分钟比较,学生的接受能力何时强一些?
分钟比较,学生的接受能力何时强一些?
(3)一个数学难题,需要 的接受能力以及
的接受能力以及 分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
(本小题满分12分)已知函数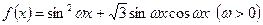 的最小正周期为
的最小正周期为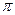 .
.
(Ⅰ)求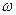 的值;
的值;
(Ⅱ)求函数f(x)的单调递增区间
本小题满分10分)已知函数 ,求
,求 的值域。
的值域。