已数列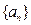 满足条件:
满足条件: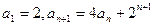 (
(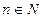 *)
*)
(Ⅰ)令 ,求证:数列
,求证:数列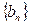 是等比数列;
是等比数列;
(Ⅱ)求数列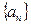 的通项公式;
的通项公式;
(Ⅲ)令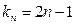 ,求数列
,求数列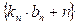 的前n项和
的前n项和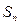 。
。
三人独立破译同一份密码.已知三人各自破译出密码的概率分别为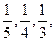 且他们是否破译出密码互不影响.
且他们是否破译出密码互不影响.
(Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.
一个袋中有6个同样大小的黑球,编好为1,2,3,4,5,6,现从中随机取出3个球,以X表示取出球的最大号码,求X的概率分布列 .
.
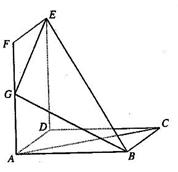
如图,已知点 是正方形
是正方形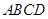 所在平面外一点,
所在平面外一点, 平面
平面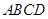 ,
,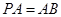 ,点
,点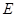 、
、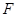 分别在线段
分别在线段 、
、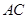 上,满足
上,满足 .
.
(1)求 与平面
与平面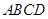 所成的角的大小;
所成的角的大小;
(2)求平面PBD与平面ABCD所成角的正切值。
(3)求证: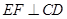 ;
;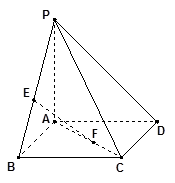
如图,在四棱锥 中,底面
中,底面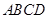 是
是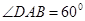 且边长为
且边长为 的菱形,侧面
的菱形,侧面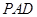 是等边三角形,且平面
是等边三角形,且平面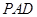 垂直于底面
垂直于底面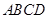 .
.
(1)若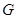 为
为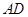 的中点,求证:
的中点,求证: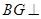 平面
平面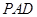 ;
;
(2)求证: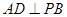 ;
;
(3)求二面角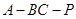 的大小.
的大小.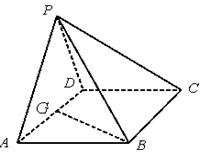
如图所示,正方形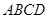 和矩形
和矩形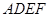 所在平面相互垂直,
所在平面相互垂直,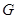 是
是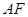 的中点.
的中点.
(I)求证: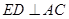 ;
;
(Ⅱ)若直线 与平面
与平面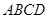 成45o角,求异面直线
成45o角,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.