(本小题满分12分)已知y=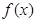 是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
(1)求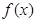 的解析式;
的解析式;
(2)求函数 的单调递减区间及值域..
的单调递减区间及值域..
已知曲线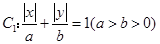 所围成的封闭图形的面积为
所围成的封闭图形的面积为 ,曲线
,曲线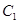 的内切圆半径为
的内切圆半径为 .记
.记 为以曲线
为以曲线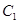 与坐标轴的交点为顶点的椭圆.
与坐标轴的交点为顶点的椭圆.
(1)求椭圆 的标准方程;
的标准方程;
(2)设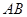 是过椭圆
是过椭圆 中心的任意弦,
中心的任意弦, 是线段
是线段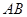 的垂直平分线.
的垂直平分线. 是
是 上异于椭圆中心的点.
上异于椭圆中心的点.
(i)若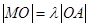 (
(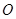 为坐标原点),当点
为坐标原点),当点 在椭圆
在椭圆 上运动时,求点
上运动时,求点 的轨迹方程;
的轨迹方程;
(ii)若 是
是 与椭圆
与椭圆 的交点,求
的交点,求 的面积的最小值.
的面积的最小值.
命题p:  ,其中
,其中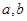 满足条件:五个数
满足条件:五个数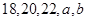 的平均数是20,标准差是
的平均数是20,标准差是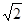 ; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆
; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆 上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。
上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L⊥直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。试建立适当的直角坐标系,解决下列问题: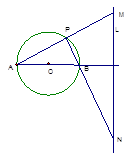
(1)若∠PAB=30°,求以MN为直径的圆方程;
(2)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。
已知抛物线 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线 :
: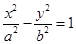 的一个焦点
的一个焦点 且垂直于
且垂直于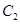 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线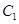 与双曲线
与双曲线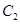 的一个交点是
的一个交点是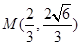 .
.
(1)求抛物线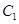 的方程及其焦点
的方程及其焦点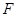 的坐标;
的坐标;
(2)求双曲线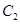 的方程及其离心率
的方程及其离心率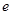 .
.
先后2次抛掷一枚骰子,将得到的点数分别记为a,b.
(1)求直线ax+by+5=0与圆x2+y2=1相切的概率;
(2)将a,b,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.