设 是由满足下列条件的函数
是由满足下列条件的函数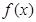 构成的集合:“①函数
构成的集合:“①函数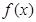 的导数
的导数 满足
满足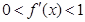 ;②方程
;②方程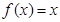 有实数根”.
有实数根”.
(I)判断函数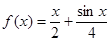 是否是集合
是否是集合 中的元素,并说明理由;
中的元素,并说明理由;
(II)集合 中的元素
中的元素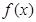 具有下面的性质:若
具有下面的性质:若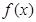 的定义域为D,则对于任意
的定义域为D,则对于任意
 D,都存在
D,都存在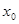

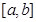 ,使得等式
,使得等式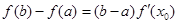 成立”,试用这一性质证明:方程
成立”,试用这一性质证明:方程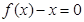 只有一个实数根;
只有一个实数根;
(III)设 是方程
是方程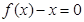 的实数根,求证:对于
的实数根,求证:对于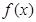 定义域中任意的
定义域中任意的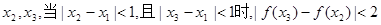 .
.
求 的最大值和最小值,
的最大值和最小值,
使式中的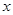 ,
, 满足约束条件
满足约束条件 .
.
用图表示不等式 表示的平面区域.
表示的平面区域.
有粮食和石油两种物资,可用轮船与飞机两种方式运输,每天每艘轮船和每架飞机的运输效果见表.
 |
轮船运输量/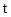 |
飞机运输量/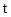 |
| 粮食 |
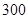 |
 |
| 石油 |
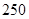 |
 |
现在要在一天内运输至少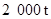 粮食和
粮食和 石油,需至少安排多少艘轮船和多少架飞机?
石油,需至少安排多少艘轮船和多少架飞机?
某运输公司接受了向抗洪救灾地区每天送至少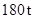 支援物资的任务.该公司有
支援物资的任务.该公司有 辆载重
辆载重 的
的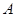 型卡车与
型卡车与 辆载重为
辆载重为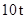 的
的 型卡车,有
型卡车,有 名驾驶员,每辆卡车每天往返的次数为
名驾驶员,每辆卡车每天往返的次数为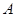 型卡车
型卡车 次,
次, 型卡车
型卡车 次;每辆卡车每天往返的成本费
次;每辆卡车每天往返的成本费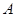 型为
型为 元,
元, 型为
型为 元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排
元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排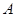 型或
型或 型卡车,所花的成本费分别是多少?
型卡车,所花的成本费分别是多少?
已知实数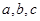 成等差数列,
成等差数列,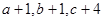 成等比数列,且
成等比数列,且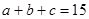 。
。
求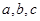 。
。