在△ABC中,角A、B、C所对的边分别是a、b、c,tanA=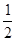 ,cosB=
,cosB= .
.
(Ⅰ)求角C;
(Ⅱ)若△ABC的最短边长是 ,求最长边的长.
,求最长边的长.
选修4—4:坐标系与参数方程
求直线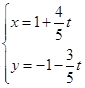 (
(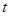 为参数)被曲线
为参数)被曲线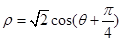 所截的弦长.
所截的弦长.
选修4-1:几何证明选讲
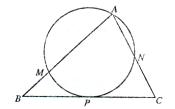
如图,已知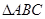 ,过顶点
,过顶点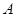 的圆与边
的圆与边 切于
切于 的中点
的中点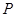 ,与边
,与边 分别交于点
分别交于点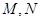 ,且
,且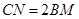 ,点
,点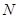 平分
平分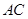 .求证:
.求证: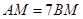 .
.
.(本小题满分12分)设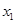 、
、
 是函数
是函数 的两个极值点。
的两个极值点。
(1)若 ,求函数
,求函数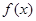 的解析式;
的解析式;
(2)若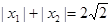 ,求
,求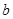 的最大值。
的最大值。
(本小题满分12分)已知某单位有50名职工,现要从中抽取10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组,按各组内抽取的编号依次增加5进行系统抽样.
(1)若第5组抽出的号码为22,写出所有被抽出职工的号码;
(2)分别统计这10名职工的体重(单位:公斤),获得体重数据的茎叶图如图所示,求该样本的方差;(温馨提示:答题前请仔细阅读卷首所给的公式)
(3)在(2)的条件下,从这10名职工中随机抽取两名体重不轻于73公斤(≥73公斤)的职工,求体重为76公斤的职工被抽取到的概率.
(本小题满分12分)如图,在三棱柱 中,
中, ⊥
⊥ ,
, ⊥
⊥ ,
, ,
, 为
为 的中点,且
的中点,且 ⊥
⊥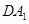 .
.
(1)求证: ⊥平面
⊥平面 ;(2)求三棱锥
;(2)求三棱锥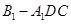 的体积.
的体积.