先化简,再求值: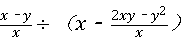 ,其中x=2,y=﹣1.
,其中x=2,y=﹣1.
.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.
(1)求该抛物线的解析式.
(2)若过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,求此直线的解析式.
(3)点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,求点P的坐标.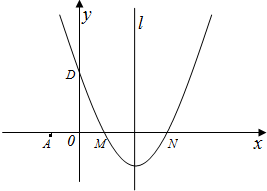
小明到一家批发兼零售的文具店给九年级学生购买考试用2B铅笔,请根据下列情景解决问题.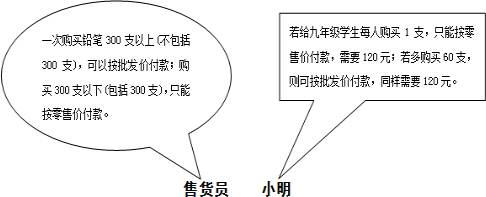
(1)这个学校九年级学生总数在什么范围内?
(2)若按批发价购买6支与按零售价购买5支的所付款相同,那么这个学校九年级学生有多少人?
在喜迎建党九十周年之际,某校举办校园唱红歌比赛,选出10名同学担任评委,并事先拟定从如下四种方案中选择合理方案来确定演唱者的最后得分(每个评委打分最高10分).
方案1:所有评委给分的平均分.
方案2:在所有评委中,去掉一个最高分和一个最低分,再计算剩余评委的平均分.
方案3:所有评委给分的中位数.
方案4:所有评委给分的众数.
为了探究上述方案的合理性,
先对某个同学的演唱成绩进行统计实验,右侧是这个同学的得分统计图:
(1)分别按上述四种方案计算这个同学演唱的最后得分.
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演唱的最后得分?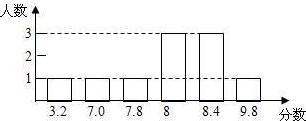
已知梯形ABCD中,AD∥BC,AB=AD(如图所示),∠BAD的平分线AE交BC于点E,连接DE.
(1)在下图中,用尺规作∠BAD的平分线AE(保留作图痕迹不写作法),并证明四边形ABED是菱形.
(2)若∠ABC=60°,EC=2BE.求证:ED⊥DC.