口袋中有大小、形状都相同的6个球,其中白球2个,红球4个,
(1)任取一个球投在一个面积为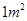 的正方形内,求球落在正方形内切圆内的概率;
的正方形内,求球落在正方形内切圆内的概率;
(2)若在袋中一次任取两个,求取到红球的概率.
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1
(1)证明:AB=AC;
(2)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小.
已知等差数列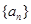 的前
的前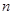 项和为
项和为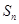 ,且
,且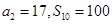 .
.
(Ⅰ)求数列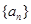 的通项公式;
的通项公式;
(Ⅱ)若数列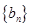 满足
满足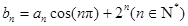 ,求数列
,求数列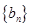 的前
的前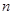 项和.
项和.
椭圆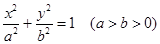 的离心率是
的离心率是 ,它被直线
,它被直线 截得的弦长是
截得的弦长是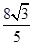 ,求椭圆的方程.
,求椭圆的方程.
已知命题p:方程 有两个不相等的实根;Q:不等式
有两个不相等的实根;Q:不等式 的解集为R;若p或Q为真,p且Q为假,求实数M的取值范围.
的解集为R;若p或Q为真,p且Q为假,求实数M的取值范围.
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, .以
.以 的中点
的中点 为球心、
为球心、 为直径的球面切
为直径的球面切 于点
于点 .
.
(1)求证:PD⊥平面 ;
;
(2)求直线 与平面
与平面 所成的角的正弦值;
所成的角的正弦值;
(3)求点 到平面
到平面 的距离.
的距离.