哈尔滨市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为 。
。
| |
优秀 |
非优秀 |
合计 |
| 甲班 |
10 |
|
|
| 乙班 |
|
30 |
|
| 合计 |
|
|
110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表: 。
。
 |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
如图,已知椭圆 的长轴为AB,过点B的直线
的长轴为AB,过点B的直线 与
与
轴垂直,椭圆的离心率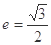 ,F为椭圆的左焦点,且
,F为椭圆的左焦点,且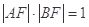

(1)求此椭圆的标准方程;
(2)设P是此椭圆上异于A,B的任意一点, 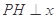 轴,H为垂足,延长HP到点Q,使得HP=PQ,连接AQ并延长交直线
轴,H为垂足,延长HP到点Q,使得HP=PQ,连接AQ并延长交直线 于点
于点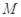 ,
,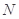 为
为 的中点,判定直线
的中点,判定直线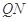 与以
与以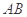 为直径的圆O位置关系。
为直径的圆O位置关系。
某地区注重生态环境建设,每年用于改造生态环境总费用为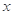 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为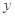 亿元。该市决定制定生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少
亿元。该市决定制定生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少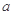 亿元,至多
亿元,至多 亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得高于每年改造生态环境总费用的25%.
亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得高于每年改造生态环境总费用的25%.
若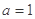 ,
,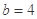 ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y= 作为生态环境改造投资方案.
作为生态环境改造投资方案.
在四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.
(1)求证:BD⊥PC;
(2)设E为PC的中点,点F在线段AB上,若直线EF∥平面PAD,求AF的长;
(3)求二面角A﹣PC﹣B的余弦值.
已知a,b,c分别是 的三个内角A,B,C的对边,
的三个内角A,B,C的对边,
(1)求A的大小;
(2)当 时,求
时,求 的取值范围.
的取值范围.
已知等差数列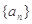 中,公差
中,公差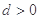 ,其前
,其前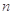 项和为
项和为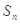 ,且满足:
,且满足: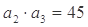 ,
, .
.
(1)求数列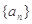 的通项公式;
的通项公式;
(2)令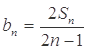 ,
,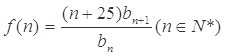 ,求
,求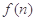 的最小值.
的最小值.