某地区注重生态环境建设,每年用于改造生态环境总费用为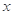 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为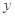 亿元。该市决定制定生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少
亿元。该市决定制定生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少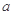 亿元,至多
亿元,至多 亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得高于每年改造生态环境总费用的25%.
亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得高于每年改造生态环境总费用的25%.
若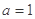 ,
,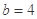 ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y= 作为生态环境改造投资方案.
作为生态环境改造投资方案.
已知函数 ,且 .
(I)试用含
的代数式表示
;
(Ⅱ)求
的单调区间;
(Ⅲ)令
,设函数
在
处取得极值,记点
,
,证明:线段
与曲线
存在异于
、
的公共点.
如图,平行四边形 中, 将 沿 折起到 的位置,使平面 平面 .
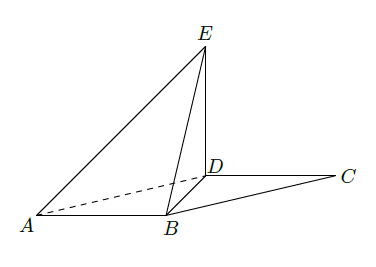
(Ⅰ)求证:
;
(Ⅱ)求三棱锥
的侧面积.
对于数列
,若存在常数
,对任意的
,恒有
,则称数列
为
数列.
(Ⅰ)首项为1,公比为
的等比数列是否为
数列?请说明理由;
(Ⅱ)设
是数列
的前
项和,给出下列两组判断:
A组:①数列
是
数列;②数列
不是
数列;
B组:③数列
是
数列;④数列
不是
数列.
请以其中一组中的一个论断为条件,另一组中的一个论断为结论组成一个命题。判断所给命题的真假,并证明你的结论;
(Ⅲ)若数列
是
数列,证明:数列
也是
数列.
已知函数
的导函数的图象关于直线
对称.
(Ⅰ)求
的值;
(Ⅱ)若
在
处取得最小值,记此极小值为
,求
的定义域和值域.
如图,在正三棱柱 中, , ,点 是 的中点,点 在 上,且 .
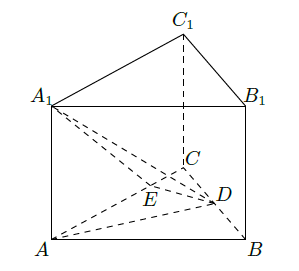
(Ⅰ)证明:平面
(Ⅱ)求直线AD和平面 所成角的正弦值。