某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上，在小-优题课

题文

某港口 $O$ 要将一件重要物品用小艇送到一艘正在航行的轮船上，在小艇出发时，轮船位于港口的 $O$ 北偏西30°且与该港口相距20海里的 $A$ 处，并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以 $v$ 海里/小时的航行速度匀速行驶，经过 $t$ 小时与轮船相遇.
（I）若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？
（II）为保证小艇在30分钟内（含30分钟）能与轮船相遇，试确定小艇航行速度的最小值；
（III)是否存在 $v$ ，使得小艇以v海里/小时的航行速度行驶，总能有两种不同的航行方向与轮船相遇？若存在，试确定v的取值范围；若不存在，请说明理由.

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

(文)已知椭圆的离心率为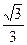，直线l：y=x+2与以原点为圆心、椭圆C₁的短半轴长为半径的圆O相切．（1）求椭圆C₁的方程；（2）设椭圆C₁的左焦点为F₁，右焦点为F₂，直线l₁过点F₁，且垂直于椭圆的长轴，动直线l₂垂直于l₁，垂足为点P，线段PF₂的垂直平分线交l₂于点M，求点M的轨迹C₂的方程；（3）过椭圆C₁的左顶点A做直线m，与圆O相交于两点R、S，若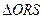是钝角三角形，求直线m的斜率k的取值范围．

(文)在某次普通测试中，为测试汉字发音水平，设置了10张卡片，每张卡片上印有一个汉字的拼音，其中恰有3张卡片上的拼音带有后鼻音“g”.
（I）现对三位被测试者先后进行测试，第一位被测试者从这10张卡片中随机抽取1张。测试后放回，余下2位的测试，也按同样的方法进行，求这三位被测试者抽取的卡片上，拼音都带有后鼻音“g”的概率：
（Ⅱ）若某位被测试者从这10张卡片中一次随机抽取3张，求这3张卡片上，拼音带有后鼻音“g”的卡片不少于2张的概率

已知函数 $f (x) = \frac{2 x - b}{(x - 1)^{2}}$ ，求导函数 $f ` (x)$ ，并确定 $f (x)$ 的单调区间．

甲、乙等五名奥运志愿者被随机地分到 $A, B, C, D$ 四个不同的岗位服务，每个岗位至少有一名志愿者．
（Ⅰ）求甲、乙两人同时参加 $A$ 岗位服务的概率；
（Ⅱ）求甲、乙两人不在同一个岗位服务的概率；
（Ⅲ）设随机变量 $ξ$ 为这五名志愿者中参加 $A$ 岗位服务的人数，求 $ξ$ 的分布列．

如图，在三棱锥 $P - A B C$ 中， $A C = B C = 2$ ， $∠ A C B = 90^{°}$ ， $A P = B P = A B$ ， $P C ⊥ A C$ ．

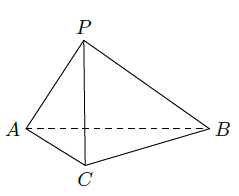
（Ⅰ）求证 $P C ⊥ A B$ ；
（Ⅱ）求二面角 $B - A P - C$ 的大小；
（Ⅲ）求点 $C$ 到平面 $A P B$ 的距离．

试卷网试题网古诗词网作文网范文网