甲、乙等五名奥运志愿者被随机地分到
四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加
岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;
(Ⅲ)设随机变量
为这五名志愿者中参加
岗位服务的人数,求
的分布列.
设函数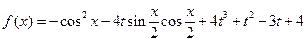 ,
,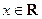 ,
,
其中|t|≤1,将f(x)的最小值记为g(t).
(1)求g(t)的表达式;
(2)对于区间[-1,1]中的某个t,是否存在实数a,使得不等式g(t)≤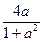 成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
已知函数f(x)=x3+ax2+b的图象在点P(1,0)处的切线与直线3x+y=0平行,
(1)求常数a、b的值;
(2)求函数f(x)在区间[0,t]上的最小值和最大值。(t>0)
已知椭圆C: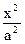 +
+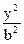 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为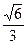 ,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
(1)求直线ON(O为坐标原点)的斜率KON ;
(2)对于椭圆C上任意一点M,试证:总存在角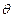 (
(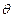 ∈R)使等式:
∈R)使等式: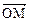 =cos
=cos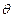
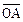 +sin
+sin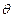
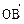 成立。
成立。
已知过点A(0,1),且方向向量为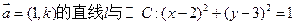 ,相交于M、N两点.
,相交于M、N两点.
(1)求实数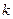 的取值范围;
的取值范围;
(2)求证: ;
;
(3)若O为坐标原点,且 .
.
学校有线网络同时提供A、B两套校本选修课程。A套选修课播40分钟,课后研讨20分钟,可获得学分5分;B套选修课播32分钟,课后研讨40分钟,可获学分4分。全学期20周,网络每周开播两次,每次均为独立内容。学校规定学生每学期收看选修课不超过1400分钟,研讨时间不得少于1000分钟。两套选修课怎样合理选择,才能获得最好学分成绩?