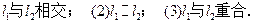如图,在长方体
中,
分别是棱
上的点(点
与
不重合),且
. 过
的平面与棱
相交,交点分别为
.
(I)证明: 平面 ;
(II)设 .在长方体 内随机选取一点.记该点取自几何体 内的概率为 ,当点 分别在棱 上运动且满足 时,求 的最小值.
甲、乙两人同时参加奥运志愿者的选拔赛,已知在备选的10道题中,甲能答对其中的6题,乙能答对其中的8题,规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才能入选.
(1)求甲答对试题数 的分布列及数学期望;
的分布列及数学期望;
(2)求甲、乙两人至少有一人入选的概率.
在 分别是角A、B、C的对边,
分别是角A、B、C的对边, ,且
,且
(1)求角B的大小;
(2)设 的最小正周期为
的最小正周期为 上的最大值和最小值.
上的最大值和最小值.
(本题满分12分)本题共有2个小题,第1小题满分5分,第2小题满分7分.
已知抛物线 ,F是焦点,直线l是经过点F的任意直线.
,F是焦点,直线l是经过点F的任意直线.
(1)若直线l与抛物线交于两点A、B,且 (O是坐标原点,M是垂足),求动点M的轨迹方程;
(O是坐标原点,M是垂足),求动点M的轨迹方程;
(2)若C、D两点在抛物线 上,且满足
上,且满足 ,求证直线CD必过定点,并求出定点的坐标.
,求证直线CD必过定点,并求出定点的坐标.
(本题满分12分)本题共有2个小题,第1小题满分5分,第2小题满分7分.
已知直线l: 与双曲线C:
与双曲线C: 相交于A、B两点.
相交于A、B两点.
(1)求实数a的取值范围;
(2)当实数a取何值时,以线段AB为直径的圆经过坐标原点.
(本题满分10分)本题共3个小题,第1小题满分4分,第2小题满分3分,第3小题满分3分.
已知直线 讨论当实数m为何值时,(1)
讨论当实数m为何值时,(1)