已知等差数列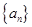 的公差
的公差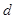 =1,前
=1,前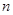 项和为
项和为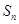 .
.
(1)若
 ;
;
(2)若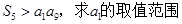 .
.
2003年10月15日9时,“神舟”五号载人飞船发射升空,于9时9分50秒准确进入预定轨道,开始巡天飞行.该轨道是以地球的中心F2为一个焦点的椭圆.选取坐标系如图所示,椭圆中心在原点.近地点A距地面200km,远地点B距地面350km.已知地球半径R=6371km.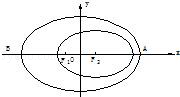
(I)求飞船飞行的椭圆轨道的方程;
(II)飞船绕地球飞行了十四圈后,于16日5时59分返
回舱与推进舱分离,结束巡天飞行,飞船共巡天飞行了约6×105km,问飞船巡天飞行的平均速度是多少km/s?
(结果精确到1km/s)(注:km/s即千米/秒)
某大桥在涨水时有最大跨度的中央桥孔如图所示,已知上部呈抛物线形,跨度为20 m,拱顶距水面6 m,桥墩高出水面4 m,现有一货船欲过此孔,该货船水下宽度不超过18 m,目前吃水线上部分中央船体高5 m,宽16 m,且该货船在现在状况下还可多装1000 t货物,但每多装150 t货物,船体吃水线就要上升0.04 m,若不考虑水下深度,该货船在现在状况下能否直接或设法通过该桥孔?为什么?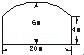
有一种电影放映机的放映灯泡的玻璃上镀铝,只留有一个透明窗用作通光孔,它的反射面是一种曲线旋转而成的曲面的一部分,灯丝定在某个地方发出光线反射到卡门上,并且这两物体间距离为4.5 cm,灯丝距顶面距离为2.8 cm,为使卡门处获得最强烈的光线,在加工这种灯泡时,应使用何种曲线可使效果最佳?试求这个曲线方程.
如图是一种加热水和食物的太阳灶,上面装有可旋转的抛物面形的反光镜,镜的轴截面是抛物线的一部分,盛水和食物的容器放在抛物线的焦点处,容器由若干根等长的铁筋焊接在一起的架子支撑.已知镜口圆的直径为12 m,镜深2 m,
(1)建立适当的坐标系,求抛物线的方程和焦点的位置;
(2)若把盛水和食物的容器近似地看作点,试求每根铁筋的长度.
根据我国汽车制造的现实情况,一般卡车高3 m,宽1.6 m.现要设计横断面为抛物线型的双向二车道的公路隧道,为保障双向行驶安全,交通管理规定汽车进入隧道后必须保持距中线0.4 m的距离行驶.已知拱口AB宽恰好是拱高OC的4倍,若拱宽为a m,求能使卡车安全通过的a的最小整数值.