2003年10月15日9时，“神舟”五号载人飞船发射升空，于9时9分50秒准确进入预定轨道，开始巡天飞行．该轨道是以地球的中心F2为一个焦点的椭圆．选取坐标系如图所示，椭圆中心在原点．近地点A距地面200km，远地点B距地面350km．已知地球半径R=6371km．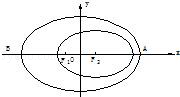
（I）求飞船飞行的椭圆轨道的方程；
（II）飞船绕地球飞行了十四圈后，于16日5时59分返
回舱与推进舱分离，结束巡天飞行，飞船共巡天飞行了约6×105km，问飞船巡天飞行的平均速度是多少km/s？
（结果精确到1km/s）（注：km/s即千米/秒）
.设椭圆C：
的左焦点为
，上顶点为
，过点作垂直于
直线交椭圆
于另外一点
,交
轴正半轴于点
，
且
⑴求椭圆的离心率；
⑵若过
三点的圆恰好与直线
相切，求椭圆C的方程. 
在数列
中,任意相邻两项为坐标的点
均在直线
上,数列
满足条件:
.
(1)求数列的通项公式;
(2)若
求
成立的正整数
的最小值.
. 如图,在四边形
中,
.
(1)求边
的长；
（2）求四边形的面积；
（3）求
的值. 
（本小题满分10分）选修4—4：坐标系与参数方程
在平面直角坐标系
中，曲线
的参数方程为
（
为参数），以坐标原点
为极点，
轴的正半轴为极轴建立极坐标系，得曲线
的极坐标方程为
（
）．
（1）化曲线、
的方程为普通方程，并说明它们分别表示什么曲线；
（2）设曲线与轴的一个交点的坐标为
（
），经过点
作曲线的切线
，求切线的方程．
.（本小题满分12分）
已知函数
.
（Ⅰ）讨论函数
的单调性；
（Ⅱ）求函数在
上的最大值.