某大桥在涨水时有最大跨度的中央桥孔如图所示,已知上部呈抛物线形,跨度为20 m,拱顶距水面6 m,桥墩高出水面4 m,现有一货船欲过此孔,该货船水下宽度不超过18 m,目前吃水线上部分中央船体高5 m,宽16 m,且该货船在现在状况下还可多装1000 t货物,但每多装150 t货物,船体吃水线就要上升0.04 m,若不考虑水下深度,该货船在现在状况下能否直接或设法通过该桥孔?为什么?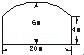
.(本小题满分14分)
已知函数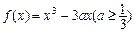 .
.
(1)当a=1时,求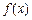 的极小值;
的极小值;
(2)设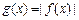 ,x∈[-1,1],求
,x∈[-1,1],求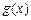 的最大值F(a).
的最大值F(a).
.(本小题满分13分)
数列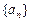 的前n项和
的前n项和 满足
满足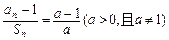 .数列
.数列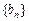 满足
满足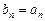 ·
·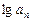 .
.
(1)求数列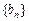 的前n项和
的前n项和 ;
;
(2)若对一切n∈N*都有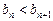 ,求a的取值范围.
,求a的取值范围.
..(本小题满分12分)
已知直线 与椭圆
与椭圆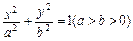 相交于A,B两点,线段AB中点M在直线
相交于A,B两点,线段AB中点M在直线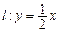 上.
上.
(1)求椭圆的离心率;
(2)若椭圆右焦点关于直线l的对称点在单位圆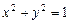 上,求椭圆的方程.
上,求椭圆的方程.
.(本小题满分12分)
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=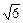
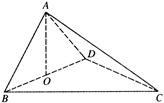
(1)求证:AO⊥平面BCD;
(2)求二面角A—BC—D的余弦值;
(3)求点O到平面ACD的距离.
.(本小题满分12分)
一个盒子里装有4张卡片,分别标有数2,3,4,5;另一个盒子里则装有分别标有3,4,5,6四个数的4张卡片.从两个盒子里各任取一张卡片.
(1)求取出的两张卡片上的数不同的概率;
(2)求取出的两张卡片上的数之和ξ的期望.