如图,已知椭圆 的长轴为AB,过点B的直线
的长轴为AB,过点B的直线 与
与
轴垂直,椭圆的离心率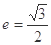 ,F为椭圆的左焦点,且
,F为椭圆的左焦点,且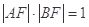

(1)求此椭圆的标准方程;
(2)设P是此椭圆上异于A,B的任意一点, 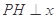 轴,H为垂足,延长HP到点Q,使得HP=PQ,连接AQ并延长交直线
轴,H为垂足,延长HP到点Q,使得HP=PQ,连接AQ并延长交直线 于点
于点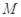 ,
,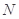 为
为 的中点,判定直线
的中点,判定直线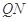 与以
与以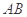 为直径的圆O位置关系。
为直径的圆O位置关系。
已知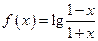 ,
,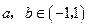 求证:
求证: .
.
已知 ,
, ,试比较
,试比较 和
和 的大小.
的大小.
设函数 上两点
上两点 、
、 ,若
,若 ,且
,且 点的横坐标为
点的横坐标为
(1)求证: 点的纵坐标为定值,并求出这个值;
点的纵坐标为定值,并求出这个值;
(2)若 ,
, ,求
,求 ;
;
(3)记 为数列
为数列 的前
的前 项和,若
项和,若 对一切
对一切 都成立,试求实数
都成立,试求实数 的取值范围。
的取值范围。
若不等式组的整数解只有-2,求a的取值范围.
假设某市 年新建住房面积
年新建住房面积 万平方米,其中有
万平方米,其中有 万平方米是中低价房.预计在今后的若干年内,该市每年新建住房面积平均比上一年增长
万平方米是中低价房.预计在今后的若干年内,该市每年新建住房面积平均比上一年增长 .另外,每年新建住房中,中低价房的面积均比上一年增加
.另外,每年新建住房中,中低价房的面积均比上一年增加 万平方米.那么,
万平方米.那么,
(1)到哪一年底,该市历年所建中低价层的累计面积(以 年为累计的第一年)将首次不少于
年为累计的第一年)将首次不少于 万平方米?
万平方米?
(2)到哪一年底,当年建造的中低价房的面积占该年建造住房面积的比例首次大于 ?
?
(参考数据: ;
; ;
; )
)