(本小题满分10分)选修4—4:坐标系与参数方程
已知曲线 的极坐标方程是
的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为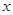 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线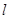 的参数方程是
的参数方程是 (
( 为参数).
为参数).
(1)求曲线 的直角坐标方程与直线
的直角坐标方程与直线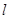 的普通方程;
的普通方程;
(2)设点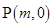 ,若直线
,若直线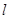 与曲线
与曲线 交于
交于 ,
,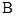 两点,且
两点,且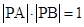 ,求实数
,求实数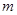 的值.[来
的值.[来
(本小题满分10分)选修4-1:几何证明选讲
如图,AB是⊙O的直径,G是AB延长线上的一点,GCD是⊙O的割线,过点G作AG的垂线,交直线AC于点E,交直线AD于点F,过点G作⊙O的切线,切点为H.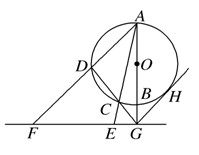
(1)求证:C,D,E,F四点共圆;
(2)若GH=6,GE=4,求EF的长.
(本小题满分12分)
己知函数 
(1)若关于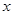 的不等式
的不等式 恒成立,求整数
恒成立,求整数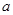 的最小值;
的最小值;
(2)若 ,正实数
,正实数 满足
满足 ,证明:
,证明: 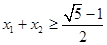
(本小题满分12分)
已知椭圆C: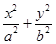 =1(
=1(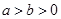 )的离心率与双曲线
)的离心率与双曲线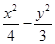 =1的一条渐近线的斜率相等,以原点为圆心,椭圆的短半轴长为半径的圆与直线
=1的一条渐近线的斜率相等,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切(
相切(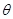 为常数).
为常数).
(1)求椭圆C的方程;
(2)若过点 的直线与椭圆
的直线与椭圆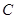 相交
相交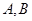 两点,设
两点,设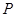 为椭圆上一点,且满足
为椭圆上一点,且满足 (
( 为坐标原点),当
为坐标原点),当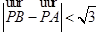 时,求实数
时,求实数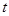 取值范围.
取值范围.
(本小题满分12分)
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,
∠BAD=∠CDA=90°,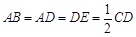 ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC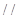 平面DMF,并说明理由;
平面DMF,并说明理由;
(2)在(1)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.