求证:当a>1时,有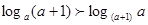
设函数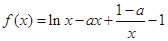 .
.
(1)当 时,求曲线
时,求曲线 在
在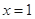 处的切线方程;
处的切线方程;
(2)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(3)在(2)的条件下,设函数 ,若对于
,若对于 ,
, ,使
,使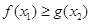 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知数列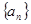 满足
满足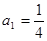 ,
, (
(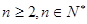 ).
).
(1)证明数列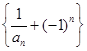 为等比数列,并求数列
为等比数列,并求数列 的通项公式;
的通项公式;
(2)设 ,求
,求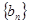 的前n项和
的前n项和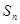 ;
;
(3)设 ,数列
,数列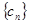 的前n项和
的前n项和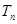 ,求证:对
,求证:对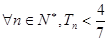 .
.
工厂有一段旧墙长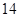 m,现准备利用这段旧墙为一面,建造平面图形为矩形,面积为
m,现准备利用这段旧墙为一面,建造平面图形为矩形,面积为 m2的厂房,工程条件是:(1)建1m新墙费用为a元;(2)修1 m旧墙费用是
m2的厂房,工程条件是:(1)建1m新墙费用为a元;(2)修1 m旧墙费用是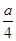 元;(3)拆去1 m旧墙,用所得材料建1m新墙费用为
元;(3)拆去1 m旧墙,用所得材料建1m新墙费用为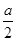 元,经过讨论有两种方案:
元,经过讨论有两种方案:
①利用旧墙的一段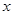
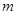 (x<14)为矩形厂房一面的边长;
(x<14)为矩形厂房一面的边长;
②矩形厂房利用旧墙的一面,矩形边长x≥14。
问:如何利用旧墙,即x为多少m时,建墙费用最省?①②两种方案哪种更好?
已知袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球 个。若从袋子中随机抽取1个小球,取到标号为2的小球的概率为
个。若从袋子中随机抽取1个小球,取到标号为2的小球的概率为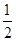 。
。
(1)求 的值;
的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球的标号为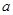 ,第二次取出的小球的标号为
,第二次取出的小球的标号为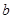 。
。
①记“ ”为事件
”为事件 ,求事件
,求事件 的概率;
的概率;
②在区间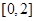 内任取2个实数
内任取2个实数 ,求时间“
,求时间“ 恒成立”的概率.
恒成立”的概率.
三棱锥P−ABC中,PA⊥平面ABC,AB⊥BC。
(1)证明:平面PAB⊥平面PBC;
(2)若 ,
, ,PB与底面ABC成60°角,
,PB与底面ABC成60°角, 分别是
分别是 与
与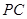 的中点,
的中点, 是线段
是线段 上任意一动点(可与端点重合),求多面体
上任意一动点(可与端点重合),求多面体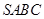 的体积.
的体积.