已知
为正实数,
为自然数,抛物线
与
轴正半轴相交于点
,设
为该抛物线在点
处的切线在
轴上的截距。
(Ⅰ)用
和
表示 ;
;
(Ⅱ)求对所有
都有
成立的
的最小值;
(Ⅲ)当
时,比较
与
的大小,并说明理由。
已知椭圆 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆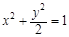 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
(1)求椭圆C的标准方程;
(2)当椭圆C的右焦点F在以AB为直径的圆内时,求k的取值范围.
已知数列{an}的前n项和为Sn,且an是Sn与2的等差中项,数列{an}中,b1=1,点P(bn,bn+1)在直线x-y+2=0上.
(Ⅰ)求数列{an},{bn}的通项公式an和bn;
(Ⅱ)设cn=an•bn,求数列{cn}的前n项和Tn
如图,在长方体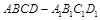 ,中,
,中,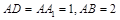 ,点
,点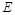 在棱AB上移动.
在棱AB上移动.
(1 )证明: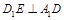 ;
;
(2)当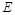 为
为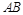 的中点时,求点
的中点时,求点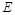 到面
到面 的距离;
的距离;
(3) 等于何值时,二面角
等于何值时,二面角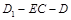 的大小为
的大小为 .
.
袋中有8个大小相同的小球,其中1个黑球,3个白球,4个红球.
(I)若从袋中一次摸出2个小球,求恰为异色球的概率;
(II)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数 都没有超过红球的个数,记此时红球的个数为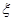 ,求
,求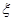 的分布列及数学期望E
的分布列及数学期望E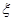 .
.
已知函数
(1)求函数 的最小正周期和最大值;
的最小正周期和最大值;
(2)求函数 单调递增区间
单调递增区间