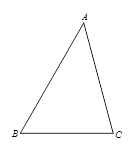
四边形ABCD是平行四边形,AB=3,AD= 5,高DE=2.建立如图所示的平面直角坐标系,其中点A与坐标原点O重合.求BC边所在直线的解析式;
设点F为直线BC与y轴的交点,求经过点B,D,F的抛物线解析式;
判断▱ABCD的对角线的交点G是否在(2)中的抛物线上,并说明理由.
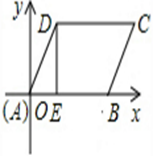
如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切, AD∥BC,连结OD,AC.
(1)求证:∠B=∠DCA;
(2)若tan B= ,OD=
,OD= , 求⊙O的半径长.
, 求⊙O的半径长.
阅读下列材料:小华遇到这样一个问题:已知:如图1,在△ABC中,AB= ,AC=
,AC= ,BC=2三边的长分别为,求∠A的正切值.
,BC=2三边的长分别为,求∠A的正切值.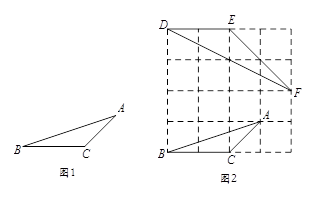
小华是这样解决问题的:如图2所示,先在一个正方形网格(每个小正方形的边长均为1)中画出格点△ABC(△ABC三个顶点都在小正方形的顶点处),然后在这个正方形网格中再画一个和△ABC相似的格点△DEF,从而使问题得解.
(1)图2中与 相等的角为,
相等的角为,  的正切值为;
的正切值为;
(2)参考小华解决问题的方法,利用图4中的正方形网格(每个小正方形的边长均为1)解决问题:如图3,在△GHK中,HK=2,HG= ,KG=
,KG= ,延长HK,求
,延长HK,求 的度数.
的度数. 
如图,⊙O的直径CD与弦AB垂直相交于点E,且BC=1,AD=2,求⊙P的直径长.
下表给出了代数式 与
与 的一些对应值:
的一些对应值:
 |
…… |
-2 |
-1 |
0 |
1 |
2 |
3 |
…… |
 |
…… |
5 |
 |
c |
2 |
-3 |
-10 |
…… |
(1)根据表格中的数据,确定 ,
, ,
, 的值;
的值;
(2)设 ,直接写出
,直接写出 时
时 的最大值.
的最大值.
如图,△ABC中,∠B=60°,∠C=75°,AC=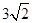 ,求AB的长.
,求AB的长.