我国云南、贵州等西南地区遇到多年不遇的旱灾.“一方有难,八方支援”为及时灌溉农田,丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台(每种至少一台)及配套相同型号抽水机4台、3台、2台,每台抽水机每小时可抽水溉农田1亩.现要求所有柴油发电机及配套抽水机同时工作—小时,灌溉农田32亩。设甲种柴油发电机数量为x台,乙种柴油发电机数量为y台.
①用含x、y的式子表示丙种柴油发电机的数量;
②求出y与x的函数关系式已知甲、乙、丙柴油发电机每台每小时费用分别为130元、120元、100元, 如何安排三种柴油发电机的数量,既能按要求抽水灌溉,同时柴油发电机总费用多少?
如图,在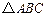 中,AB是
中,AB是 的直径,
的直径, 与AC交于点D,
与AC交于点D,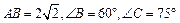 ,
,
求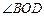 的度数;
的度数;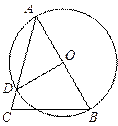
解方程: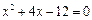 .
.
某射击运动员在相同条件下的射击160次,其成绩记录如下:
| 射击次数 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
| 射中9环以上的次数 |
15 |
33 |
63 |
79 |
97 |
111 |
130 |
|
| 射中9环以上的频率 |
0.75 |
0.83 |
0.80 |
0.79 |
0.79 |
0.79 |
0.81 |
(1)根据上表中的信息将两个空格的数据补全(射中9环以上的次数为整数,频率精确到0.01);
(2)根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1),
并简述理由.
阅读下列材料,并回答问题.
画一个直角三角形,使它的两条直角边分别为5和12,那么我们可以量得直角三角形的斜边长为13,并且 。事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方。如果直角三角形中,两直角边长分别为a、b,斜边长为c,则
。事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方。如果直角三角形中,两直角边长分别为a、b,斜边长为c,则 ,这个结论就是著名的勾股定理.
,这个结论就是著名的勾股定理.
请利用这个结论,完成下面的活动:
(1)一个直角三角形的两条直角边分别为6、8,那么这个直角三角形斜边长为.
(2)满足勾股定理方程 的正整数组(a,b,c)叫勾股数组。例如(3,4,5)就是一组勾股数组。观察下列几组勾股数
的正整数组(a,b,c)叫勾股数组。例如(3,4,5)就是一组勾股数组。观察下列几组勾股数
① 3, 4, 5 ; ② 5,12,13 ; ③ 7,24,25 ;④ 9,40,41 ;
请你写出有以上规律的第⑤组勾股数:.
(3)如图,AD⊥BC于D,AD=BD,AC=BE。AC=3,DC=1,求BD的长度.
(4)如图,点A在数轴上表示的数是,请用类似的方法在下图数轴上画出表示数 的B点(保留作图痕迹).
的B点(保留作图痕迹).
在ABC中,AB=AC,∠BAC=120°,AD⊥AC于点A,
(1)求∠BAD的度数.
(2)证明:DC=2BD.