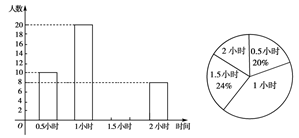
为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时。为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:在这次调查中共调查了多少名学生?
求户外活动时间为1.5小时的人数,并补充频数分布直方图;
求表示户外活动时间1小时的扇形圆心角的度数;
本次调查中学生参加户外活动的平均时间是否符合要求?请说明理由。
(1)阅读合作学习内容,解答其中的问题;
| 合作学习 如图,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=3,另两边与反比例函数 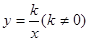 的图象分别相交于点E,F,且DE=2,过点E作EH⊥ 的图象分别相交于点E,F,且DE=2,过点E作EH⊥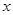 轴于点H,过点F作FG⊥EH于点G。回答下列问题: 轴于点H,过点F作FG⊥EH于点G。回答下列问题: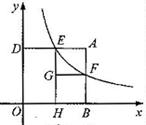 ①该反比例函数的解析式是什么? ②当四边形AEGF为正方形时,点F的坐标是多少? |
(2)小亮进一步研究四边形AEGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”针对小亮提出的问题,请你判断这两个矩形能否全等?直接写出结论即可;这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由。
甲乙两件服装的进价共500元,商场决定将甲服装按30%的利润定价,乙服装按20%的利润定价,实际出售时,两件服装均按9折出售,商场卖出这两件服装共获利67元.
(1)求甲乙两件服装的进价各是多少元;
(2)由于乙服装畅销,制衣厂经过两次上调价格后,乙服装每件的进价达到242元,求每件乙服装进价的平均增长率;
(3)若每件乙服装进价按平均增长率再次上调,商场仍按9折出售,此时定价至少为多少元时,乙服装才可获得利润(定价取整数)?
如图,已知点O为△ABC的内心,连AO、BO、CO,过点O的直线分别交边AB、AC于点M、N,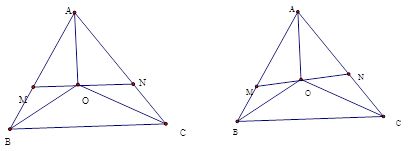
图一图二
(1)若∠BAC=70°,那么∠BOC=°;
(2)如图1,若MN∥BC,BM=2,CN=3,求线段MN的长;
(3)如图2,若MN⊥AO,BM=2,CN=3,求线段MN的长.
如图,AB是⊙O的直径,点F、C是⊙O上两点,且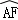 =
=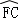 =
= ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.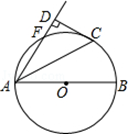
(1)求证:CD是⊙O的切线;
(2)若CD=2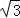 ,求⊙O的半径.
,求⊙O的半径.
已知关于x的方程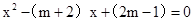 .
.
(1)求证:方程恒有两个不相等的实数根 ;
(2)若此方程的一个根是1,请求出方程的另一个根,并直接写出以这两根为直角边的直角三角形外接圆半径的值。