如图，在平面直角坐标系xoy中，抛物线y＝
x2－
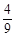x－10与x轴的交点为A，与y轴的交点为点B，过点B作x轴的平行线BC，交抛物线于点C，连结AC．现有两动点P，Q分别从O，C两点同时出发，点P以每秒4个单位的速度沿OA向终点A移动，点Q以每秒1个单位的速度沿CB向点B移动，点P停止运动时，点Q也同时停止运动．线段OC，PQ相交于点D，过点D作DE∥OA，交CA于点E，射线QE交x轴于点F．设动点P，Q移动的时间为t(单位：秒)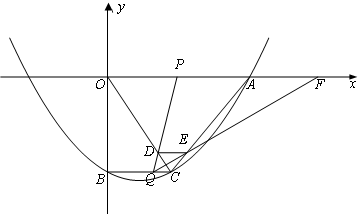
（1）求A，C两点的坐标和抛物线的顶点M坐标；
（2）当t为何值时，四边形PQCA为平行四边形？请写出计算过程；
（3）当0<t<4.5时，△PQF的面积是否总为定值？若是，求出此定值；若不是，请说明理由；
（4）当t为何值时，△PQF为等腰三角形？请写出解答过程．
如图1，平面直角坐标系中，抛物线
与
轴交于A、B两点，点C是AB的中点，CD⊥AB且CD=AB.直线BE与
轴平行，点F是射线BE上的一个动点，连接AD、AF、DF.
（1）若点F的坐标为（
，
），AF=
.
①求此抛物线的解析式；
②点P是此抛物线上一个动点，点Q在此抛物线的对称轴上，以点A、F、P、Q为顶点构成的四边形是平行四边形，请直接写出点Q的坐标；
（2）若
，
，且AB的长为
，其中
.如图2，当∠DAF=45时，求
的值和∠DFA的正切值.
以平面上一点O为直角顶点，分别画出两个直角三角形，记作△AOB和△COD，其中∠ABO=∠DCO=30．
图1 图2 图3
（1）点E、F、M分别是AC、CD、DB的中点，连接FM、EM．
①如图1，当点D、C分别在AO、BO的延长线上时，
=_______；
②如图2，将图1中的△AOB绕点O沿顺时针方向旋转
角（
），其他条件不变，判断的值是否发生变化，并对你的结论进行证明；
（2）如图3，若BO=
，点N在线段OD上，且NO=2.点P是线段AB上的一个动点，在将△AOB绕点O旋转的过程中，线段PN长度的最小值为_______，最大值为_______．
已知抛物线
经过点（
，
）．
（1）求
的值；
（2）若此抛物线的顶点为（
，
），用含
的式子分别表示和，并求与之间的函数关系式；
（3）若一次函数
，且对于任意的实数
，都有
≥
，直接写出
的取值范围.
阅读下面的材料：
小明在学习中遇到这样一个问题：若1≤x≤m，求二次函数
的最大值．他画图研究后发现，
和
时的函数值相等，于是他认为需要对
进行分类讨论．
他的解答过程如下：
∵二次函数的对称轴为直线
，
∴由对称性可知，和时的函数值相等．
∴若1≤m＜5，则时，
的最大值为2；
若m≥5，则
时，的最大值为
．
请你参考小明的思路，解答下列问题：
（1）当
≤x≤4时，二次函数
的最大值为_______；
（2）若p≤x≤2，求二次函数的最大值；
（3）若t≤x≤t+2时，二次函数的最大值为31，则
的值为_______．
平面直角坐标系
中，原点O是正三角形ABC外接圆的圆心，点A在
轴的正半轴上，△ABC的边长为6．以原点O为旋转中心将△ABC沿逆时针方向旋转角，得到△
，点
、
、
分别为点A、B、C的对应点．
（1）当=60时，
①请在图1中画出△；
②若AB分别与
、
交于点D、E，则DE的长为_______；
（2）如图2，当⊥AB时，分别与AB、BC交于点F、G，则点的坐标为 _____，△FBG的周长为_____，△ABC与△重叠部分的面积为_______．