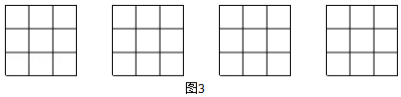
小明和小亮用如图所示的两个转盘做游戏,转动两个转盘各一次。若两次数字和为奇数,则小明得1分;而若和为偶数,则小亮得1分。这个游戏对双方公平吗?为什么?(请用列表法说明理由)。如果不公平,如何修改规则,使游戏对双方都公平。
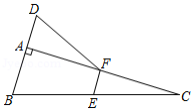
如图,已知:在 中, ,延长 到点 ,使 ,点 , 分别是边 , 的中点.求证: .
先化简: ,再从1,2,3中选取一个适当的数代入求值.
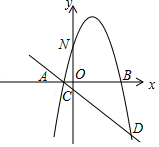
如图,抛物线 与 轴交于 、 两点 在 的左侧),与 轴交于点 ,过 点的直线 与 轴交于点 ,与抛物线 的另一个交点为 ,已知 , , 点为抛物线 上一动点(不与 、 重合).
(1)求抛物线和直线 的解析式;
(2)当点 在直线 上方的抛物线上时,过 点作 轴交直线 于点 ,作 轴交直线 于点 ,求 的最大值;
(3)设 为直线 上的点,探究是否存在点 ,使得以点 、 , 、 为顶点的四边形为平行四边形?若存在,求出点 的坐标;若不存在,请说明理由.
如图,在 中, , , , 平分 , 交 于点 , 交 于点 , 的外接圆 交 于点 ,连接 .
(1)求证: 是 的切线;
(2)求 的半径 及 的正切值.

在数学活动课上,王老师要求学生将图1所示的 正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)
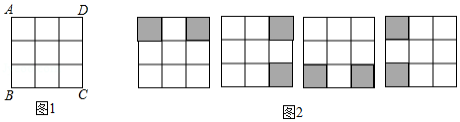
请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个 的正方形方格画一种,例图除外)