已知函数f(x)=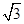 sin(ωx+φ) (0<φ<π,ω>0)过点
sin(ωx+φ) (0<φ<π,ω>0)过点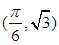 ,函数y=f(x)图象的两相邻对称轴间的距离为
,函数y=f(x)图象的两相邻对称轴间的距离为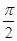 .
.
(1) 求f(x)的解析式;
(2) f(x)的图象向右平移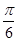 个单位后,得到函数y=g(x)的图象,求函数g(x)的单调递减区间.
个单位后,得到函数y=g(x)的图象,求函数g(x)的单调递减区间.
如图,在直三棱柱 中,
中,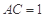 ,
,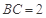 ,
,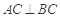 ,
, 分别为棱
分别为棱 的中点.
的中点.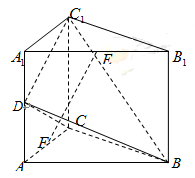
(Ⅰ)求证: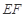 ∥平面
∥平面 ;
;
(Ⅱ)若异面直线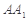 与
与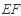 所成角为
所成角为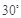 ,求三棱锥
,求三棱锥 的体积.
的体积.
设数列{an}满足:a1=1,an+1=3an,n∈N*.设Sn为数列{bn}的前n项和, 已知b1≠0,2bn–b1=S1 Sn,n∈N*.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=bn log3 an,求数列{cn}的前n项和Tn .
选修4—5:不等式选讲
已知关于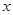 的不等式
的不等式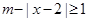 ,其解集为
,其解集为 .
.
(Ⅰ)求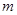 的值;
的值;
(Ⅱ)若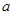 ,
, 均为正实数,且满足
均为正实数,且满足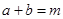 ,求
,求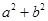 的最小值.
的最小值.
选修4-4:坐标系与参数方程
已知平面直角坐标系 中,以
中,以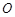 为极点,
为极点, 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线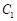 方程为
方程为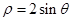 .
. 的参数方程为
的参数方程为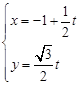 (
( 为参数).
为参数).
(Ⅰ)写出曲线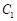 的直角坐标方程和
的直角坐标方程和 的普通方程;
的普通方程;
(Ⅱ)设点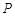 为曲线
为曲线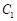 上的任意一点,求点
上的任意一点,求点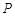 到曲线
到曲线 距离的取值范围.
距离的取值范围.
选修4—1:几何证明选讲
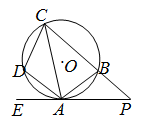
如图,四边形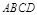 内接于⊙
内接于⊙ ,过点
,过点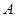 作⊙
作⊙ 的切线EP交CB的延长线于P,已知
的切线EP交CB的延长线于P,已知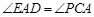 .
.
证明(Ⅰ)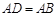 ;
;
(Ⅱ)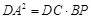 .
.