已知f(x)=x2-2x-ln(x+1)2.
(1)求f(x)的单调递增区间;
(2)若函数F(x)=f(x)-x2+3x+a在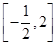 上只有一个零点,求实数a的取值范围.
上只有一个零点,求实数a的取值范围.
已知公差不为0的等差数列{an},a1=1,且a2,a4-2,a6成等比数列.
(1)求数列{an}的通项公式;
(2)已知数列{bn}的通项公式是bn=2n-1,集合A={a1,a2,…,an,…},B={b1,b2,b3,…,bn,…}.将集合A∩B中的元素按从小到大的顺序排成一个新的数列{cn},求数列{cn}的前n项和Sn.
如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC.把△BAC沿AC折起到△PAC的位置,使得点P在平面ADC上的正投影O恰好落在线段AC上,如图2所示.点E、F分别为棱PC,CD的中点.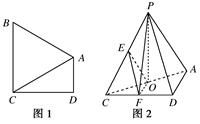
(1)求证:平面OEF∥平面APD;
(2)求证:CD⊥平面POF;
(3)在棱PC上是否存在一点M,使得M到P,O,C,F四点距离相等?请说明理由.
某高校组织自主招生考试,其有2 000名学生报名参加了笔试,成绩均介于195分到275分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),……,第八组[265,275).如图是按上述分组方法得到的频率分布直方图.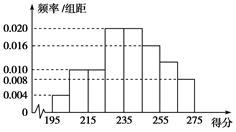
(1)从这2 000名学生中,任取1人,求这个人的分数在255~265之间的概率约是多少?
(2)求这2 000名学生的平均分数;
(3)若计划按成绩取1 000名学生进入面试环节,试估计应将分数线定为多少?
设函数f(x)=sin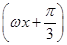 +sin
+sin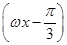 +
+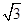 cos ωx(其中ω>0),且函数f(x)的图象的两条相邻的对称轴间的距离为
cos ωx(其中ω>0),且函数f(x)的图象的两条相邻的对称轴间的距离为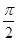 .
.
(1)求ω的值;
(2)将函数y=f(x)的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在区间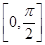 上的最大值和最小值.
上的最大值和最小值.