设函数f(x)＝sin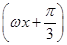
＋sin
＋
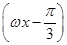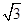cos ωx(其中ω＞0)，且函数f(x)的图象的两条相邻的对称轴间的距离为
.
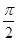(1)求ω的值；
(2)将函数y＝f(x)的图象上各点的横坐标伸长到原来的2倍，纵坐标不变，得到函数y＝g(x)的图象，求函数g(x)在区间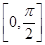
上的最大值和最小值．
设函数
，
（1）求f（x）的周期；
（2）当x∈[﹣π，π]时，求f（x）单调递增区间；
（3）当x∈[0，2π]时，求f（x）的最大值和最小值．
已知椭圆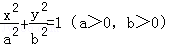
的左焦点F为圆x2+y2+2x=0的圆心，且椭圆上的点到点F的距离最小值为
．
（Ⅰ）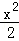
+y2=1；
（Ⅱ）已知经过点F的动直线l与椭圆交于不同的两点A、B，点M（
），证明：
为定值．
已知△ABC中，角A，B，C所对的边分别是a，b，c，且2（a2+b2﹣c2）=3ab；
（1）求
；
（2）若c=2，求△ABC面积的最大值．
已知数列{an}的各项均为正数，Sn是数列{an}的前n项和，且4Sn=an2+2an﹣3．
（1）求数列{an}的通项公式；
（2）已知bn=2n，求Tn=a1b1+a2b2+…+anbn的值．
设函数f（x）=ax2+（b﹣2）x+3（a≠0）
（1）若不等式f（x）＞0的解集（﹣1，3）．求a，b的值；
（2）若f（1）=2，a＞0，b＞0求
+
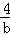的最小值．