设函数f(x)=ax2+(b﹣2)x+3(a≠0)
(1)若不等式f(x)>0的解集(﹣1,3).求a,b的值;
(2)若f(1)=2,a>0,b>0求 +
+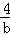 的最小值.
的最小值.
如图,AB为⊙O的直径,直线CD与⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.
证明:
(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
如图,已知圆上的弧 ,过C点的圆的切线与BA的延长线交于E点,
,过C点的圆的切线与BA的延长线交于E点,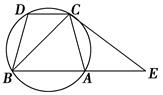
证明:
(1)∠ACE=∠BCD;
(2)BC2=BE·CD.
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t该农产品.以X(单位: t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x∈[100,110),则取X=105,且X=105的概率等于需求量落入[100,110)的频率,求T的数学期望.
某工科院校对A,B两个专业的男女生人数进行调查,得到如下的列联表:
| 专业A |
专业B |
总计 |
|
| 女生 |
12 |
4 |
16 |
| 男生 |
38 |
46 |
84 |
| 总计 |
50 |
50 |
100 |
(1)从B专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
(2)能否在犯错误的概率不超过0.05的前提下,认为工科院校中“性别”与“专业”有关系呢?
注:K2=
| P(K2≥k0) |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
| k0 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h),试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5
2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4
1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5
(1)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(2)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?