如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC.把△BAC沿AC折起到△PAC的位置,使得点P在平面ADC上的正投影O恰好落在线段AC上,如图2所示.点E、F分别为棱PC,CD的中点.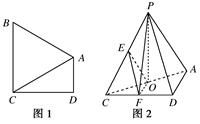
(1)求证:平面OEF∥平面APD;
(2)求证:CD⊥平面POF;
(3)在棱PC上是否存在一点M,使得M到P,O,C,F四点距离相等?请说明理由.
A.(选修4—1:几何证明选讲)
如图,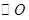 的半径
的半径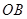 垂直于直径
垂直于直径 ,
,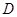 为
为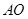 上一点,
上一点, 的延长线交
的延长线交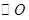 于点
于点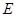 ,
,
过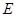 点的圆的切线交
点的圆的切线交
 的延长线于
的延长线于 .求证:
.求证: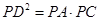 .
.
(本小题满分16分) [已知数列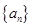 满足
满足 ,
,
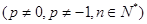 .
.
(1)求数列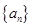 的通项公式
的通项公式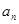 ;
;
(2)若对每一个正整数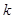 ,若将
,若将 按从小到大的顺序排列后,此三项均能构成等
按从小到大的顺序排列后,此三项均能构成等
差数列, 且公差为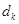 .①求
.①求 的值及对应的数列
的值及对应的数列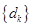 .
.
②记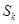 为数列
为数列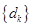 的前
的前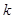 项和,问是否存在
项和,问是否存在 ,使得
,使得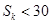 对任意正整数
对任意正整数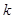 恒成立?若存
恒成立?若存
在,求出 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
(本小题满分16分)
对于函数 ,若存在实数对(
,若存在实数对(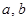 ),使得等式
),使得等式 对定义域中的每
对定义域中的每
一个 都成立,则称函数
都成立,则称函数
 是“(
是“(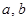 )型函数”.
)型函数”.
(1)判断函数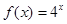 是否为“(
是否为“(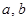 )型函数”,并说明理由;
)型函数”,并说明理由;
(2)已知函数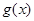 是“(1,4)型函数”, 当
是“(1,4)型函数”, 当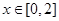 时,都有
时,都有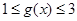 成立,且当
成立,且当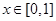
时,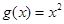
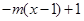
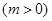 ,若,试求
,若,试求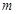 的取值范围.
的取值范围.
(本小题满分16分)如图,在平面直角坐标系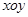 中,已知点
中,已知点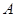 为椭圆
为椭圆 的右顶点, 点
的右顶点, 点 ,点
,点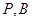 在椭圆上,
在椭圆上,  .
.
(1)求直线 的
的 方程; (2)求直线
方程; (2)求直线 被过
被过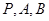 三点的圆
三点的圆 截得的弦长;
截得的弦长;
(3)是否存在分别以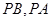 为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不
为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不
存在,请说明理由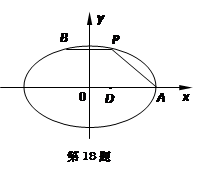
(本小题满分14分)
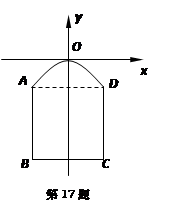
在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对
称图形),其中矩形 的三边
的三边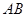 、
、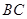 、
、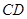 由长6分米的材料弯折而成,
由长6分米的材料弯折而成,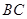 边的长
边的长
为 分米(
分米(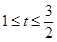 );曲线
);曲线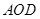 拟从以下两种曲线中选择一种:曲线
拟从以下两种曲线中选择一种:曲线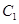 是
是 一段余弦曲线
一段余弦曲线
(在如图所示的平面直角坐标系中,其解析式为 ),此时记门的最高点
),此时记门的最高点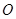 到
到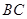
边的距离为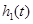 ;曲线
;曲线 是一段抛物线,其焦点到准线的距离为
是一段抛物线,其焦点到准线的距离为 ,此时记门的最高点
,此时记门的最高点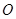
到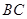 边的距离为
边的距离为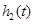 .
.
(1)试分别求出函数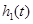 、
、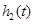 的表达式;
的表达式;
(2)要使得点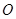 到
到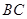 边的距离最大,应选用哪一种曲线?此时,最大值是多少?
边的距离最大,应选用哪一种曲线?此时,最大值是多少?