(本小题满分16分) [已知数列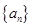 满足
满足 ,
,
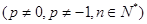 .
.
(1)求数列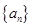 的通项公式
的通项公式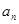 ;
;
(2)若对每一个正整数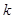 ,若将
,若将 按从小到大的顺序排列后,此三项均能构成等
按从小到大的顺序排列后,此三项均能构成等
差数列, 且公差为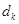 .①求
.①求 的值及对应的数列
的值及对应的数列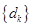 .
.
②记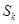 为数列
为数列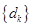 的前
的前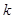 项和,问是否存在
项和,问是否存在 ,使得
,使得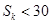 对任意正整数
对任意正整数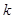 恒成立?若存
恒成立?若存
在,求出 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
(本小题满分12分)已知椭圆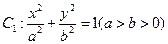 的左、右焦点分别为
的左、右焦点分别为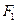 、
、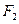 ,其中
,其中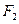 也是抛物线
也是抛物线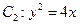 的焦点,
的焦点,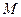 是
是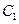 与
与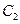 在第一象限的交点,且
在第一象限的交点,且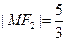 .
.
(1)求椭圆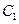 的方程;
的方程;
(2)已知菱形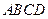 的顶点
的顶点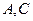 在椭圆
在椭圆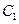 上,顶点
上,顶点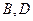 在直线
在直线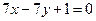 上,求直线
上,求直线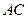 的方程.
的方程.
(本小题满分12分)已知数列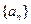 、
、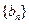 满足
满足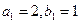 ,且
,且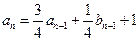 ,
,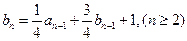
(1)令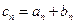 ,求数列
,求数列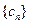 的通项公式;
的通项公式;
(2)求数列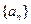 的通项公式及前
的通项公式及前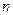 项和公式
项和公式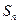 .
.
(本小题满分12分)如图,四棱锥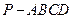 中,侧面PDC是边长为2的正三角形,且与底面
中,侧面PDC是边长为2的正三角形,且与底面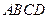 垂直,底面ABCD是面积为
垂直,底面ABCD是面积为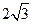 的菱形,
的菱形,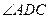 为锐角,M为PB的中点。
为锐角,M为PB的中点。
(1)求证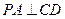
(2)求二面角 的大小
的大小
(3)求P到平面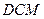 的距离
的距离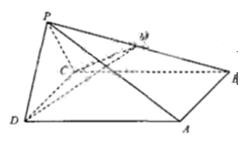
(本小题满分13分)某校要用三辆汽车从新校区把教职工接到老校区,已知从新校区到老校区有两条公路,汽车走公路①堵车的概率为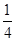 ,不堵车的概率为
,不堵车的概率为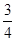 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为 ,不堵车的概率为
,不堵车的概率为 .若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
.若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
(Ⅰ)若三辆汽车中恰有一辆汽车被堵的概率为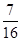 ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(Ⅱ)在(1)的条件下,求三辆汽车中被堵车辆的个数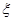 的分布列和数学期望
的分布列和数学期望
(本小题满分12分)已知函数 的最小正周期为
的最小正周期为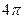 .
.
(1)求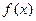 的单调递增区间;
的单调递增区间;
(2)在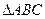 中,角
中,角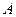 ,
,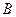 ,
,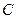 的对边长分别是
的对边长分别是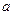 ,
, ,
, 满足
满足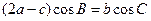 ,求函数
,求函数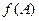 的取值范围.
的取值范围.