(本小题满分12分)已知椭圆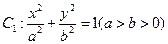 的左、右焦点分别为
的左、右焦点分别为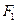 、
、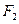 ,其中
,其中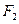 也是抛物线
也是抛物线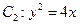 的焦点,
的焦点,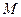 是
是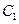 与
与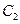 在第一象限的交点,且
在第一象限的交点,且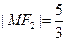 .
.
(1)求椭圆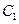 的方程;
的方程;
(2)已知菱形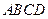 的顶点
的顶点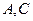 在椭圆
在椭圆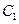 上,顶点
上,顶点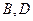 在直线
在直线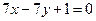 上,求直线
上,求直线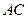 的方程.
的方程.
(本小题满分14分)如图,长方体ABCD—A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
(1)求证:直线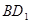 ∥平面
∥平面 ;
;
(2)求证:平面
 平面
平面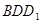 ;
;
(3)求三棱锥D—PAC的体积。
(本小题满分14分)已知 ,
,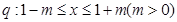 ,若
,若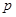 是
是 的充分不必要条件,求
的充分不必要条件,求 的取值范围。
的取值范围。
(本小题满分16分)已知三条直线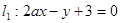 ,
, 和
和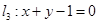 ,
,
(1)若此三条直线不能构成三角形,求实数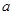 的取值范围;
的取值范围;
(2)已知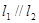 ,能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到
,能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到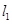 的距离是P点到
的距离是P点到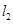 的距离的
的距离的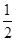 ;③P点到
;③P点到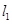 的距离与P点到
的距离与P点到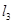 的距离之比是
的距离之比是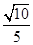 。若能,试求P点坐标;若不能,请说明理由。
。若能,试求P点坐标;若不能,请说明理由。
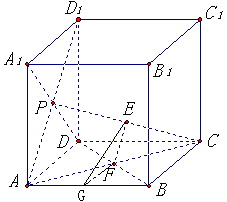
(本小题满分16分) 在正方体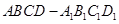 中,
中,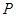 为侧面
为侧面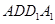 的中心,
的中心,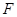 为底面
为底面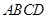 的中心,
的中心,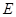 为
为 的中点,G为AB的 中点,
的中点,G为AB的 中点,
(1)求证:平面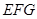 //平面
//平面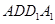 ;
;
(2)求证:平面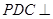 平面
平面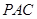 .
.
(本小题满分16分)某商品的市场需求量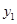 (万件)、市场供应量
(万件)、市场供应量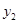 (万件)与市场价格x(元/件)分别近似的满足下列关系:
(万件)与市场价格x(元/件)分别近似的满足下列关系: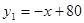 ,
, ,当
,当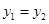 时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量。
时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量。
(1)求平衡价格和平衡需求量;
(2)若要使平衡需求量增加6万件,政府对每件商品应给予多少元补贴?
(3)求当每件商品征税6元时新的平衡价格?