(本小题满分14分)
在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对
称图形),其中矩形 的三边
的三边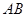 、
、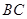 、
、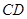 由长6分米的材料弯折而成,
由长6分米的材料弯折而成,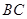 边的长
边的长
为 分米(
分米(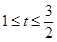 );曲线
);曲线 拟从以下两种曲线中选择一种:曲线
拟从以下两种曲线中选择一种:曲线 是
是 一段余弦曲线
一段余弦曲线
(在如图所示的平面直角坐标系中,其解析式为 ),此时记门的最高点
),此时记门的最高点 到
到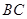
边的距离为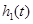 ;曲线
;曲线 是一段抛物线,其焦点到准线的距离为
是一段抛物线,其焦点到准线的距离为 ,此时记门的最高点
,此时记门的最高点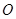
到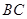 边的距离为
边的距离为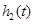 .
.
(1)试分别求出函数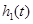 、
、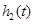 的表达式;
的表达式;
(2)要使得点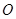 到
到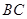 边的距离最大,应选用哪一种曲线?此时,最大值是多少?
边的距离最大,应选用哪一种曲线?此时,最大值是多少?
(本小题满分12分)已知某校 四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从
四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从 四个社团的学生当中随机抽取10名学生参加问卷调查.
四个社团的学生当中随机抽取10名学生参加问卷调查.
(Ⅰ)从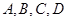 四个社团中各抽取多少人?
四个社团中各抽取多少人?
(Ⅱ)在社团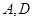 所抽取的学生总数中,任取2个,求
所抽取的学生总数中,任取2个,求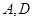 社团中各有1名学生的概率.
社团中各有1名学生的概率.
【改编】(本小题满分12分)已知数列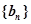 的前
的前 项和为
项和为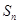 ,满足
,满足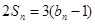
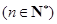 .
.
(Ⅰ)求数列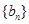 的通项公式;
的通项公式;
(Ⅱ)求数列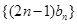 的前n项和
的前n项和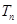 .
.
(本小题满分13分)椭圆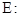
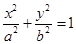 (
( )的左焦点为
)的左焦点为 ,右焦点为
,右焦点为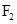 ,离心率
,离心率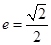 .设动直线
.设动直线
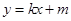 与椭圆
与椭圆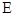 相切于点
相切于点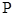 且交直线
且交直线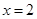 于点
于点 ,
,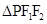 的周长为
的周长为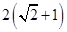 .
.
(1)求椭圆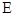 的方程;
的方程;
(2)求两焦点 、
、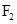 到切线
到切线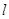 的距离之积;
的距离之积;
(3)求证:以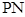 为直径的圆恒过点
为直径的圆恒过点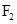
【原创】已知函数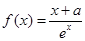 .
.
(Ⅰ)若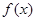 在区间
在区间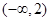 上为单调递增函数,求实数
上为单调递增函数,求实数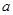 的取值范围;
的取值范围;
(Ⅱ)若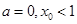 ,设直线
,设直线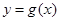 为函数
为函数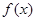 的图象在
的图象在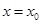 处的切线,求证:
处的切线,求证: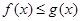 .
.
(本小题满分13分)已知数列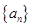 的前
的前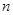 项之和为
项之和为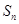 (
(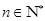 ),且满足
),且满足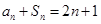 .
.
(1)求证:数列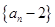 是等比数列,并求数列
是等比数列,并求数列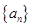 的通项公式;
的通项公式;
(2)求证: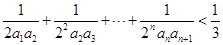 .
.